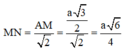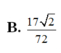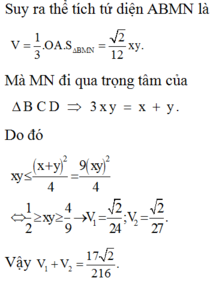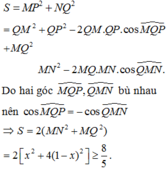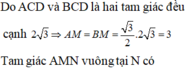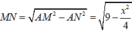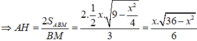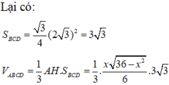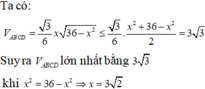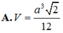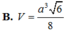Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
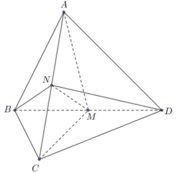
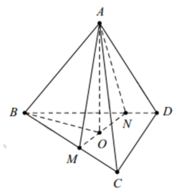
Gọi M, N lần lượt là trung điểm của BD, AC. Đặt BD = 2x, AC = 2y (x, y > 0).
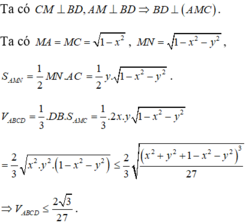

Chọn B

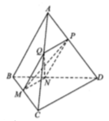
Gọi M, N lần lượt là trung điểm AD và BC.
Theo giả thiết ta có: ABD và ACD là các tam giác cân có M là trung điểm của AD nên:
![]()
Và có BM=CM => ΔMBC cân tại M
Trong tam giác ΔMBC có MN vừa là đường cao vừa là trung tuyến nên

Khi đó diện tích tam giác ΔMBC là:

Thể tích tứ diện ABCD là:

Đặt AD=x, BC=y ta có:

Dấu bằng xảy ra khi x=y.
Ta lại có:

Dấu bằng xảy ra khi:

Vậy giá trị lớn nhất của thể tích khối tứ diện ABCD là:


Đáp án B
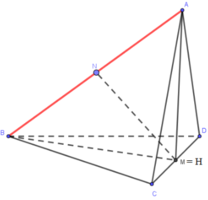
Cách giải:
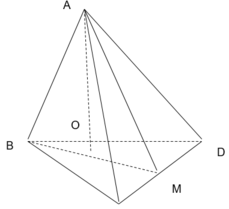
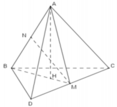
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD)) ⇒ H ∈ BM, AH ⊥ HM
VABCD lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M
Hai tam giác ACD, BCD đều, cạnh a, có đường cao AM, BM bằng a 3 2
Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB ⇒ MN ⊥ AB
Mà MN ⊂ (AMB) ⊥ CD ⇒ MN ⊥ CD ⇒ MN là đoạn vuông góc chung của AB và CD
Khoảng cách giữa hai đường thẳng AB và CD là: