Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.

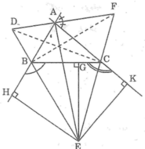
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.

a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>AE=HE
c: BA=BH
EA=EH
=>BE là trung trực của AH
d: BE là trung trực của AH
=>BE vuông góc AH
Ta có �D thuộc phân giác của �^A;
��⊥��DH⊥AB; ��⊥��DK⊥AC ⇒��=��⇒DH=DK (tính chất tia phân giác của một góc).
Gọi �G là trung điểm của ��BC.
Xét △���△BGD và △���△CGD, có
���^=���^=90∘BGD=CGD=90∘ (��DG là trung trực của ��BC ),
��=��BG=CG (già thiết),
��DG là cạnh chung.
Do đó △���=△���△BGD=△CGD (hai cạnh góc vuông)
⇒��=��⇒BD=CD (hai cạnh tương ứng).
Xét △���△BHD và △���△CKD, có
���^=���^=90∘BHD=CKD=90∘ (giả thiết);
��=��DH=DK (chứng minh trên);
��=��BD=CD (chứng minh trên).
Do đó △���=△���△BHD=△CKD (cạnh huyền - cạnh góc vuông)
⇒��=��⇒BH=CK (hai cạnh tương ứng).
Ta có DD thuộc phân giác của \widehat{A}A;
D H \perp A BDH⊥AB; D K \perp A CDK⊥AC \Rightarrow D H=D K⇒DH=DK (tính chất tia phân giác của một góc).
Gọi GG là trung điểm của BCBC.
Xét \triangle B G D△BGD và \triangle C G D△CGD, có
\widehat{B G D}=\widehat{C G D}=90^{\circ}BGD=CGD=90∘ (DGDG là trung trực của B CBC ),
BG=CGBG=CG (già thiết),
DGDG là cạnh chung.
Do đó \triangle B G D=\triangle C G D△BGD=△CGD (hai cạnh góc vuông)
\Rightarrow B D=C D⇒BD=CD (hai cạnh tương ứng).
Xét \triangle B H D△BHD và \triangle C K D△CKD, có
\widehat{B H D}=\widehat{C K D}=90^{\circ}BHD=CKD=90∘ (giả thiết);
D H=D KDH=DK (chứng minh trên);
B D=C DBD=CD (chứng minh trên).
Do đó \triangle B H D=\triangle C K D△BHD=△CKD (cạnh huyền - cạnh góc vuông)
\Rightarrow B H=C K⇒BH=CK (hai cạnh tương ứng).