Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEH vuông tại E và ΔAHB vuông tại H có
góc EAH chung
=> ΔAEH đồng dạng với ΔAHB
b: ΔAHB vuông tại H có HE vuông góc AB
nên AH^2=AE*AB
ΔAHC vuông tại H
mà HF là đường cao
nên AF*AC=AH^2=AE*AB
c: AE*AB=AF*AC
=>AE/AC=AF/AB
=> ΔAEF đồng dạng với ΔACB
d: Xét ΔMEB và ΔMCF có
góc MEB=góc MCF
góc M chung
=> ΔMEB đồng dạng với ΔMCF
=>ME/MC=MB/MF
=>ME*MF=MB*MC

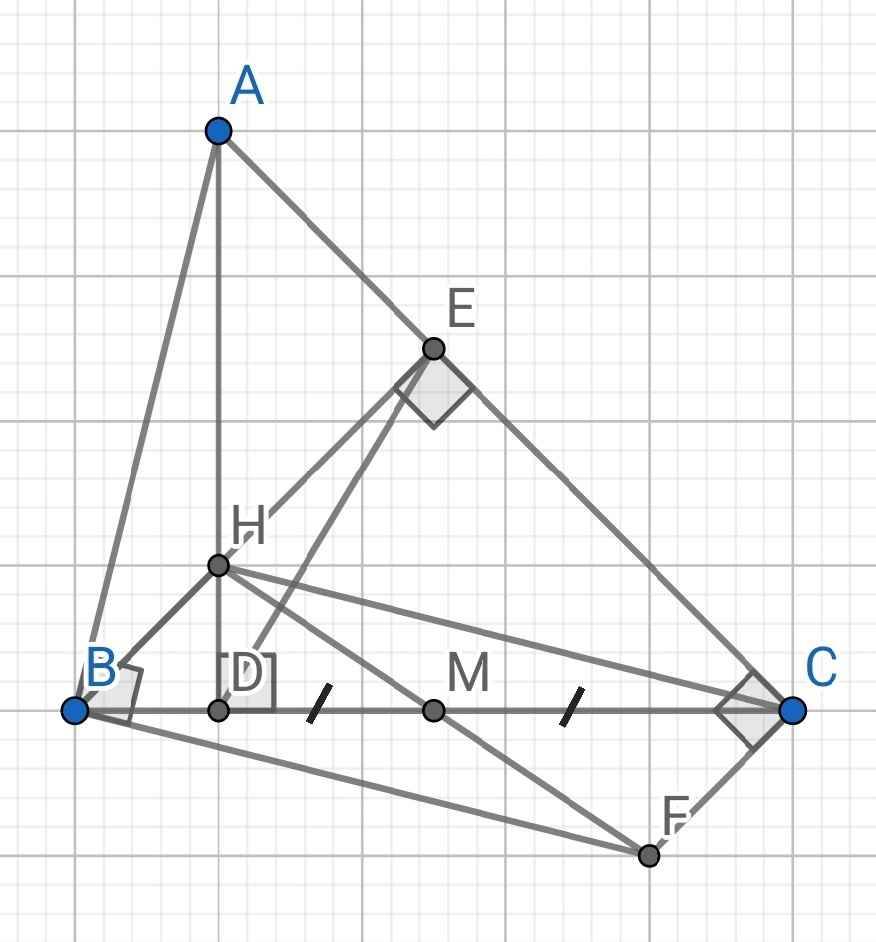 d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
⇒ CH là đường cao thứ ba của ∆ABC
⇒ CH ⊥ AB
Mà BF ⊥ AB (gt)
⇒ CH // BF
Do CF ⊥ AC (gt)
BE ⊥ AC (gt)
⇒ CF // BE
⇒ CF // BH
Tứ giác BHCF có:
CH // BF (cmt)
CF // BH (cmt)
⇒ BHCF là hình bình hành
e) Do BHCF là hình bình hành (cmt)
Mà M là trung điểm của đường chéo BC (gt)
⇒ M là trung điểm của đường chéo HF
⇒ H, M, F thẳng hàng

a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACH}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
b) Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=AC^2-AH^2=30^2-24^2=324\)
hay HC=18(cm)
Ta có: ΔABC∼ΔHAC(cmt)
nên \(\dfrac{AB}{HA}=\dfrac{BC}{AC}=\dfrac{AC}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{AB}{24}=\dfrac{BC}{30}=\dfrac{30}{18}=\dfrac{5}{3}\)
Suy ra: \(\left\{{}\begin{matrix}\dfrac{AB}{24}=\dfrac{5}{3}\\\dfrac{BC}{30}=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=40\left(cm\right)\\BC=50\left(cm\right)\end{matrix}\right.\)
Vậy: HC=18cm; AB=40cm; BC=50cm

1: Xet ΔABC và ΔHBA có
góc ABC chung
góc BAC=góc BHA
=>ΔABC đồng dạng với ΔHBA
2: \(BC=\sqrt{12^2+16^2}=20\)
AH=16*12/20=9,6
BH=12^2/20=7,2
3: góc AMN=góc HMB=90 độ-góc CBN
góc ANM=90 độ-góc ABN
mà góc CBN=góc ABN
nên góc AMN=góc ANM
=>ΔAMN cân tại A

a, Xét tam giác AHE và ABH có :
\(+,\widehat{AEH}=\widehat{AHB}=90^0\)
\(+,\widehat{HAB}chung\)
Vậy tam giác \(AHE~ABH\left(g.g\right)\)
b,
Theo hệ thức lượng trong tam giác vuông ta có :
\(AH^2=AE.AB=AF.AC\)
Vậy \(\frac{AE}{AC}=\frac{AF}{AB}\left(1\right)\)
Xét tam giác AEF và ACB có :
\(+,\)góc A chung
\(+,\left(1\right)\)
\(\Rightarrow\Delta AEF~ACB\left(c.g.c\right)\)
c, Tự làm nhé

Bấn vô chỗ này hộ mk !
V
CHỖ NÀO