Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chia A thành 3 tập hợp:
B={1;4;7}; C={2;5;8}; D={0;3;6}
TH1: 2 số trong B, 2 số trong C
=>Có \(C^2_3\cdot C^2_3\cdot4!=216\left(cách\right)\)
TH2: 1 số trong B, 1 số trong C, số 0 và 1 số trong D
=>Có 3*3*1*2*3*3*2*1=324 cách
TH3: 1 số trong B, 1 số trong C, 2 số khác 0 trong D
=>Có 3*3*1*4!=216 cách
TH4: 3 số trong B, số 0
=>Có 3*3*2*1=18 cách
TH5: 3 số trong B, 1 số khác 0 trong D
=>Có 2*4!=24*2=48 cách
TH6: 3 số trong C, số 0
=>Có 3*3*2*1=18 cách
TH7: 3 số trong C, 1 số khác 0 trong D
=>Có 2*4!=48 cách
=>Có 216+324+216+18+48+18+48=888 cách

a) Số có ba chữ số khác nhau có thể lập được là: 6.5.4 = 120 (số)
b) Số chia hết cho 3 nên tổng 3 chữ số chia hết cho 3, có các cặp số là: (1,2,3), (1,2,6), (2,3,4), (3,4,5), (4,5,6), (1,5,6), (1,3,5), (2,4,6).
Số có ba chữ số khác nhau và chia hết cho 3 có thể lập được là:
8. 3! = 48 (số)

a) Xét trường hợp các chữ số đều bình đẳng :
Số cách sắp xếp 2 chữ số lẻ khác nhau từ A cho 4 vị trí :
\(C_3^1.C_4^1.C_2^1.C_3^1=72\)
Số cách sắp xếp 2 chữ số chẵn từ A cho 2 vị trí còn lại A :
\(C_4^1.C_2^1.C_3^1.C_1^1=24\)
=> Có tất cả : 72.24 = 1728 số
Xét trường hợp cố định số 0 đứng đầu
=> Số cách sắp xếp 2 chữ số lẻ từ A cho 3 vị trí :
\(C_3^1.C_3^1.C_2^1.C_2^1=36\)
Số cách sắp xếp 1 chữ số chẵn từ A cho vị trí còn lại :
\(C_3^1.C_1^1=3\)
=> Có tất cả : 1.36.3 = 108 số
=> Số các số thỏa mãn đề : 1728 - 108 = 1620 (số)
b) Gọi số thỏa mãn có dạng \(\overline{abcd}\)
TH1 a = 3 => b \(\in\left\{4;5;6\right\}\) hoặc b = 2
(*) \(b\in\left\{4;5;6\right\}\) => Số các số cần tìm : \(1.C_3^1.A_5^2=60\)
(*) b = 2 => Số các số cần tìm : \(1.1.1.C_2^1+1.1.1.C_4^1=6\)
TH1 có 66 số
TH2 \(a\in\left\{4;5;6\right\}\)
TH2 có : \(C_3^1.A_6^3=360\)
Vậy có tất cả 360 + 66 = 426

Gọi số cần tìm là \(\overline{abcd}\)
TH1 : a = 6
Số cách chọn chữ số a : 1 cách
Số cách chọn chữ số b : 2 cách
Số cách chọn chữ số c,d : \(A^2_6\)
=> Số các số lập được \(1.2.A^2_6\)
TH2 : a = 7 hoặc a = 8
=> Số các số là : \(2.A^3_7\)
Vậy có tất cả : \(P=1.2.A^2_6+2.A_7^3=480\) số

Tổng S của 5 chữ số lập từ tập trên luôn thỏa mãn
\(0+1+2+3+4\le S\le9+8+7+6+5\)
\(\Rightarrow10\le S\le35\)
Mà S chia hết cho 9 \(\Rightarrow S=\left\{18;27\right\}\) (lưu ý rằng 2 số này cộng lại đúng bằng 45, do đó giả sử nếu ta chọn được S=18 như 1;2;3;4;8 chia hết cho 5 thì phần còn lại chính là S=27 tương ứng)
Gọi tập S=18 là A, tập S=27 là B, ta chọn tập A:
TH1: A chứa 0 mà ko chứa 9, chọn 4 chữ số còn lại tổng 18:
- Các cặp 18; 27; 36; 45 tổng bằng 9 nên chọn 2 trong 4 cặp này có \(C_4^2=6\) cách
Hoán vị 5 chữ số tập A có \(5!-4!\) cách \(\Rightarrow6.\left(5!-4!\right)=576\) số tập A
Hoán vị 5 chữ số tập B tương ứng có \(5!\) cách \(\Rightarrow6.5!=720\) số tập B
- Các bộ 1467; 2358 tổng bằng 18, có 2 cách chọn 1 bộ
Hoán vị 5 chữ số tập A \(\Rightarrow2.\left(5!-4!\right)=192\) số
Hoán vị 5 chữ số tập B tương ứng: \(2.5!=240\) số
TH2: A chứa 9 mà ko chứa 0:
\(\Rightarrow\) Chọn 4 chữ số còn lại có tổng bằng 9, dễ dàng thấy ko có bộ nào thỏa mãn do 1+2+3+4>9
TH3: A chứa cả 0 lẫn 9:
\(\Rightarrow\) Tổng 3 chữ số còn lại bằng 9, ta có các bộ 126; 135; 234; có 3 bộ
Hoán vị 5 chữ số của A: \(3\left(5!-4!\right)=288\) số
Hoán vị 5 chữ số tập B: \(3.5!=360\) số
TH4: A ko chứa cả 0 lẫn 9:
Có các bộ 12348; 12357; 12456 tổng 3 bộ
Hoán vị tập A: có \(3.5!=360\) số
Hoán vị tập B : \(3.\left(5!-4!\right)=288\) số
\(\Rightarrow\text{576+720+192+240+288+360+360+288=3024}\) số
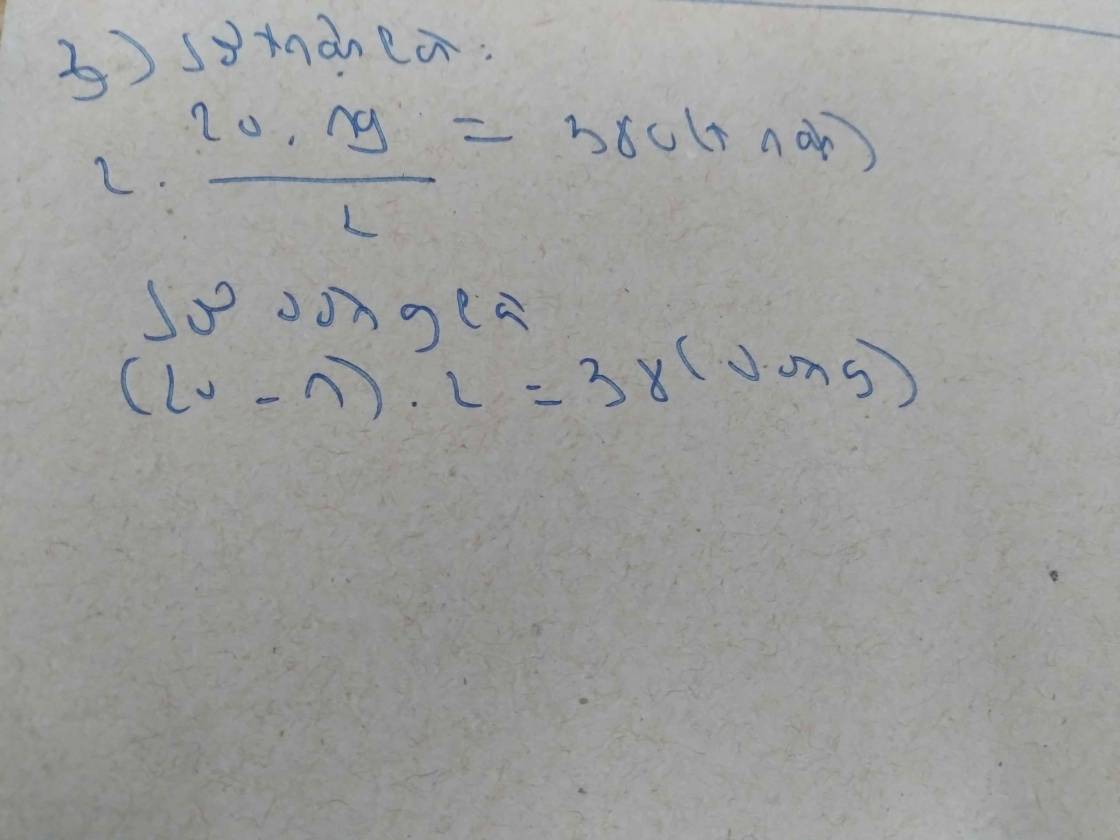
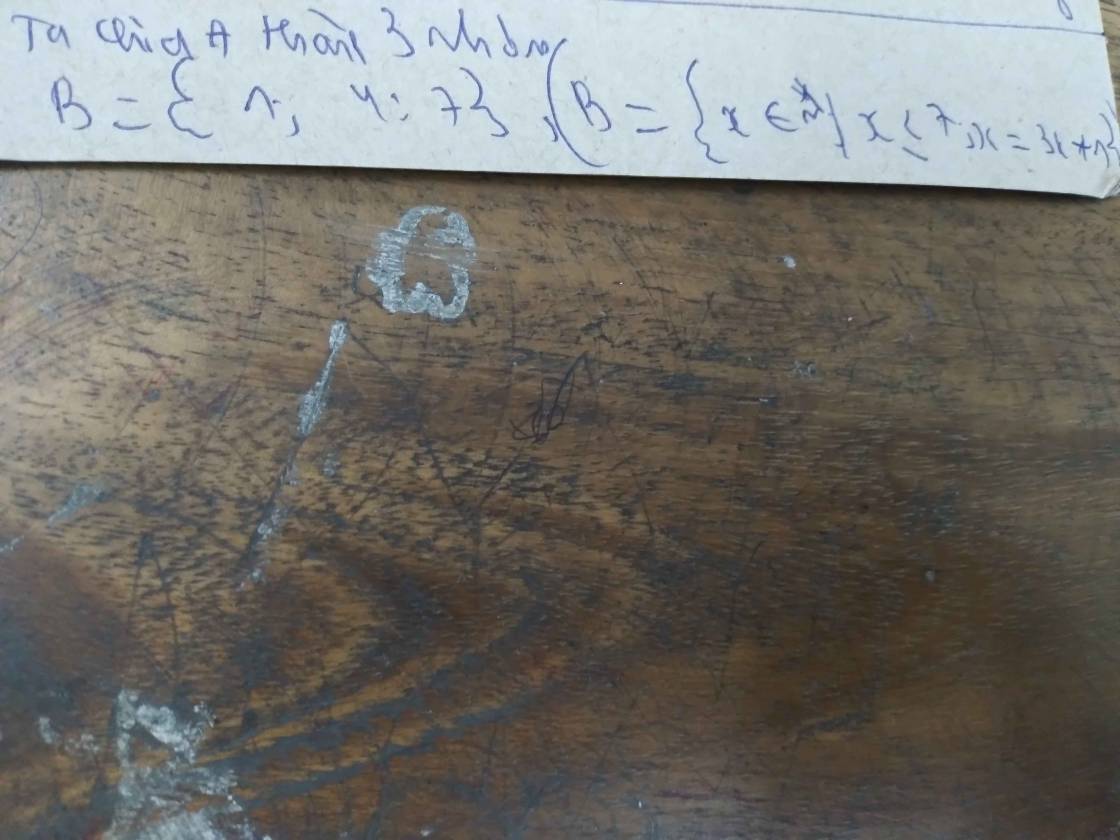



Khi lập một số từ 1 tập sao cho chia hết cho 3 thì thường đầu tiên là ta sẽ chia tập hợp ban đầu thành 3 tập nhỏ theo số dư khi chia 3: tập B={0;3;6} gồm 3 phần tử là các số chia 3 dư 0, tập C={1;4} chia 3 dư 1, tập D={2;5} chia 3 dư 2
4 chữ số chia hết cho 3 khi tổng của nó chia hết cho 3, ta có các trường hợp: 2B+1C+1D (nghĩa là 2 phần tử thuộc B+1 phần tử thuộc C+1 phần tử thuộc D), 2C+2D
Chỉ có 2 cách trên là thỏa mãn
TH1: 2B1C1D:
- Nếu trong 2 phần tử B có xuất hiện số 0: có 2 cách chọn (02;06), chọn 1C có 2 cách, chọn 1D có 2 cách
Hoán vị 4 chữ số sao cho số 0 ko đứng đầu: 4!-3! cách
Tổng cộng theo quy tắc nhân: \(2.2.2.\left(4!-3!\right)=144\) số
- Nếu 2 phần tử B ko xuất hiện số 0: có 1 cách chọn (3;6), chọn 1C có 2 cách, 1D có 2 cách
Hoán vị 4 chữ số: \(4!\) cách
Tổng: \(1.2.2.4!=96\)
TH2: 2C2D có đúng 1 cách chọn 2 chữ số từ C và 2 chữ số từ D
Hoán vị 4 chữ số này: \(4!=24\) số
Vậy có: \(144+96+24=264\) số
Ủa em đã học tới tổ hợp chưa nhỉ? Chương trình mới là lớp 10 có học tổ hợp đúng ko?