
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tập A có n phần tử:
Số tập con có 3 phân tử là: \(C_n^3=\frac{n!}{3!\left(n-3\right)!}=\frac{n\left(n-1\right)\left(n-2\right)}{6}\)
Số tập con 2 phần tử là : \(C_n^2=\frac{n!}{2!\left(n-2\right)!}=\frac{n\left(n-1\right)}{2}\)
Theo bài ra ta có: \(\frac{n\left(n-1\right)\left(n-2\right)}{6}-\frac{n\left(n-1\right)}{2}=14\)<=> \(n^3-6n^2+5n-84=0\Leftrightarrow n=7\)
Vậy tập A có 7 phần tử

Số tổ hợp con có x phần tử là số tổ hợp chập x của 5.
=> Số tổ hợp con có lẻ phần tử là: \(C_5^1 + C_5^3 + C_5^5=5+10+1=16\)
Số tổ con có chẵn phần tử là: \(C_5^0 + C_5^2 + C_5^4=1+10+5=16\)
\( \Rightarrow C_5^0 + C_5^2 + C_5^4 = C_5^1 + C_5^3 + C_5^5\) (đpcm)

Số tập con của A: \(2^7\)
Số tập con có ít hơn 3 phần tử của A gồm: rỗng, 1 phần tử, 2 phần tử
Có: \(1+C_7^1+C_7^2=29\) tập như vậy
Vậy có \(2^7-29=99\) tập thỏa mãn yêu cầu đề bài

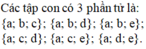
Do tập hợp A có 5 phần tử nên số tập con của tập hợp A là: \({2^5} = 32\) (tập con)