Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(f(x)=(-x+1)(x-2)>0\Leftrightarrow \left\{\begin{matrix} -x+1< 0\\ x-2< 0\end{matrix}\right.\) hay $1< x< 2$
hay $x\in (1;2)$
Đáp án D

(x+1)(x-m)<=0
TH1: m>=0
=>-1<=x<=m
=>m>5
TH2: m<0
(x+1)(x-m)<=0
*Trường hợp 1: x+1>=0 và x-m<=0
=>-1<=x<=m
=>m<0
=>\(m\in\varnothing\)
*TH2: x+1<=0và x-m>=0
=>x<=-1 và x>=m
=>m>5

Lời giải:
\(f(x)>0\Leftrightarrow 2x-4>0\Leftrightarrow 2x>4\Leftrightarrow x>2\) hay \(x\in (2;+\infty)\)
Suy ra khẳng định $a$ đúng

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)
\(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)
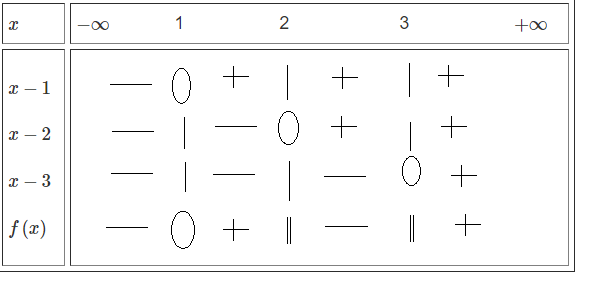
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)
\(\Rightarrow B.\)

Phương trình \({x^2} - 2x - 3 = 0\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 3\)
Có \(a = 1 > 0\) nên
\(f\left( x \right) = {x^2} - 2x - 3 > 0\) khi và chỉ khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
=> Phát biểu a) đúng.
\(f\left( x \right) = {x^2} - 2x - 3 < 0\) khi và chỉ khi \(x \in \left( { - 1;3} \right)\)
=> Phát biểu b) sai vì khi x=-1 hoặc x=3 thì \({x^2} - 2x - 3 = 0\) (không nhỏ hơn 0).
\(\text{f(x)}\)\(\text{>0}\)\(\text{⇔}\)\(\text{2x}\)2\(\text{-3x+1}\)\(>0\)⇔\(\left\{{}\begin{matrix}x>1\\x< \dfrac{1}{2}\end{matrix}\right.\)
⇒x∈(−∞;\(\dfrac{1}{2}\))∪(1;+∞)