Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác vuông HBD có \(BH=\sqrt{BD^2-DH^2}=\sqrt{5^2-4^2}=3\)
Từ A hạ AM vuông góc với BC, ta có DH//AM (vì cùng vuông góc với BC)
D là trung điểm của AB và DH//AM => DH là đường trung bình của tam giác BAM => H là trung điểm của BM => BM=2.DH=2.3=6.
BC = 12 => MC = BC - BM = 12 - 6 =6 => BM = MC => M là trung điểm của BC
AM vừa là đường cao, vừa là trung tuyến => Tam giác ABC cân tại A
X

Bạn xem lời giải ở đây:
Câu hỏi của cao ngoc khanh linh - Toán lớp 7 - Học toán với OnlineMath

Bạn xem lời giải ở đây:
Câu hỏi của cao ngoc khanh linh - Toán lớp 7 - Học toán với OnlineMath

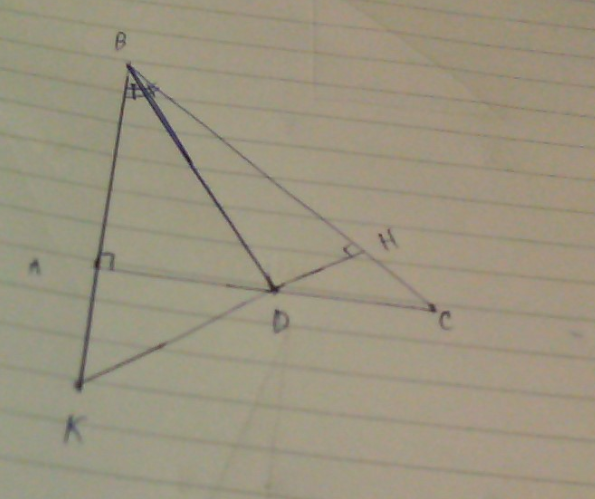
Xét \(\triangle ABD\) vuông tại \(A\) và \(\triangle HBD\) vuông tại H \(( DH \bot BC)\) ta có :
\(\widehat{ABD}=\widehat{HBD}\) ( tia phân giác của \(\widehat{ABC}\) cắt \(AC\) tại \(D\) )
Chung \(BD\)
\(\Rightarrow\) \(\triangle ABD\) \(=\) \(\triangle HBD\) ( ch - gn )
\(\Rightarrow AB = BH\) ( \(2\) cạnh tương ứng ) (1)
Do \(\begin{cases} \widehat{BAD} = 90^o\\ \widehat{BHD} = 90^0\end{cases}\)
\(\Rightarrow \widehat{KAD} = \widehat{CHD} = 90^o\)
Xét \(\triangle AKD\) vuông tại \(A\) và \(\triangle HCD\) vuông tại \(H\) ta có :
\(\widehat{ADK} = \widehat{HDC}\) ( \(2\) góc đối đỉnh )
\(AD=DH \) ( \(\triangle ABD = \) \(\triangle HBD\) )
\(\Rightarrow\) \(\triangle AKD=\) \(\triangle HCD\) ( cgv - gnk )
\(\Rightarrow AK = CH\) ( \(2\) cạnh tương ứng ) (2)
Từ (1) và (2)
\(\Rightarrow AB+AK = BH+CH\)
\(\Leftrightarrow BK=BC\)
\(\Rightarrow \triangle KBC\) cân tại \(B\)