Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

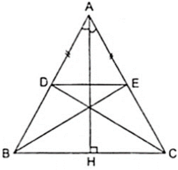
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.

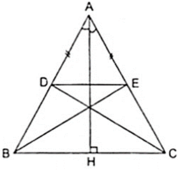
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.

a) Xét ∆AHD và ∆FHA có:
^AHD = ^FHA (= 900)
\(\frac{AH}{HD}=\frac{HF}{AH}\)(gt)
Do đó ∆AHD ~ ∆FHA (c.g.c)
⇒ ^HAD = ^HFA
Mà ^HFA + ^FAH = 900 nên ^HAD + ^FAH = 900 ⇒ ^FAD = 900
Vậy ∆ADF vuông tại A (đpcm)
b) Đặt AC = CD = a thì AB = 2a
∆ABC vuông tại A nên BC2 = AB2 + AC2 = (2a)2 + a2 = 5a2 ⇒ \(BC=a\sqrt{5}\)
Ta có: BD = BC - CD \(=a\sqrt{5}-a\Rightarrow BD^2=a^2\left(\sqrt{5}-1\right)^2=a^2\left(6-2\sqrt{5}\right)\)(1)
và AE = AB - BE = AB - BD = AB - (BC - CD) = AB - BC + CD \(=2a-a\sqrt{5}+a=\left(3-\sqrt{5}\right)a\)
\(\Rightarrow AB.AE=2a.\left(3-\sqrt{5}\right)a=a^2\left(6-2\sqrt{5}\right)\)(2)
Từ (1) và (2) suy ra BD2 = AB.AE (đpcm)

a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Xét ΔAEB có
H là trung điểm của EB
M là trung điểm của AB
Do đó: HM là đường trung bình
=>HM//AE và HM=AE/2
hay HD//AE và HD=AE
hay ADHE là hình bình hành