Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc FEQ=góc FMQ=90 độ
=>FMEQ nội tiếp
Tam I là trung điểm của FQ

a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>AC=4(cm)
Xét ΔBCD vuông tại B có BA là đường cao
nên \(BA^2=AC\cdot AD\)
=>\(4\cdot AD=3^2=9\)
=>AD=2,25(cm)
b: ΔBAC vuông tại A có AE là đường cao
nên \(BE\cdot BC=BA^2\left(1\right)\)
Xét ΔBAD vuông tại A có AF là đường cao
nên \(BF\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BE\cdot BC=BF\cdot BD\)
c: BE*BC=BF*BD
=>\(\dfrac{BE}{BD}=\dfrac{BF}{BC}\)
Xét ΔBEF vuông tại B và ΔBDC vuông tại B có
\(\dfrac{BE}{BD}=\dfrac{BF}{BC}\)
Do đó: ΔBEF đồng dạng với ΔBDC
=>\(\widehat{BFE}=\widehat{BCD}\)

Tứ giác AEHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 o nên DE = AH.
Xét ABC vuông tại A có: A H 2 = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A

Tứ giác ARHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 ∘ nên DE = AH.
Xét ∆ ABC vuông tại A có A H 2 = HB.HC = 4.9 = 36 ⇔ AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D

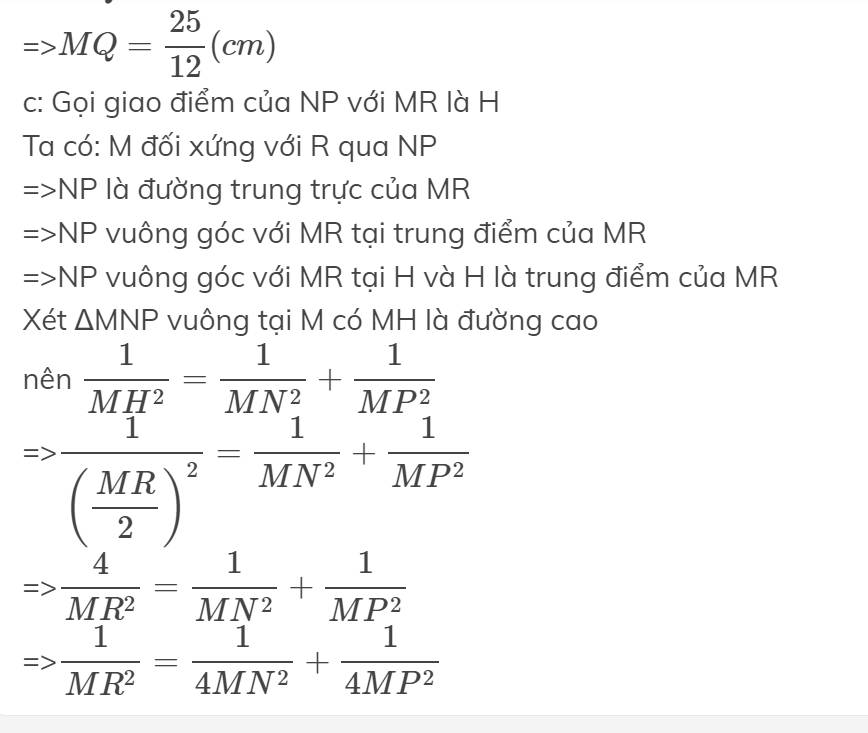
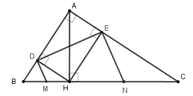
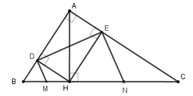
1: ΔNMQ vuông tại N
=>\(NM^2+NQ^2=QM^2\)
=>\(NM^2=5^2-3^2=16\)
=>NM=4(cm)
Xét ΔNMQ vuông tại N có
\(sinM=\dfrac{NQ}{MQ}=\dfrac{3}{5}\)
=>\(\widehat{NMQ}\simeq37^0\)
ΔNMQ vuông tại N
=>\(\widehat{NMQ}+\widehat{NQM}=90^0\)
=>\(\widehat{NQM}=90^0-37^0=53^0\)
Xét ΔQMD vuông tại Q có QN là đường cao
nên \(QN^2=NM\cdot ND\)
=>\(ND\cdot4=3^2=9\)
=>ND=2,25(cm)
MQ=MN+ND
=4+2,25
=6,25(cm)
ΔMQD vuông tại Q
=>\(MQ^2+QD^2=MD^2\)
=>\(QD^2=6,25^2-5^2=14,0625\)
=>QD=3,75(cm)
3: ΔQMN vuông tại N có NE là đường cao
nên \(QE\cdot QM=QN^2\left(1\right)\)
Xét ΔQND vuông tại N có NF là đường cao
nên \(QF\cdot QD=QN^2\left(2\right)\)
Từ (1) và (2) suy ra \(QE\cdot QM=QF\cdot QD\)
b:
Xét ΔNQD vuông tại N có NF là đường cao
nên \(NF\cdot QD=NQ\cdot ND;DF\cdot FQ=NF^2\)
=>\(NF=\dfrac{3\cdot2.25}{3.75}=1,8\left(cm\right)\)
Xét ΔMNQ vuông tại N có NE là đường cao
nên \(NE^2=EM\cdot EQ;NE\cdot MQ=NQ\cdot NM\)
=>\(NE\cdot5=3\cdot4=12\)
=>NE=2,4(cm)
\(ME\cdot EQ+DF\cdot FQ\)
\(=NE^2+NF^2\)
\(=2,4^2+1,8^2=9\)