Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: NP=15cm
b: Xét ΔDFE có \(EF^2=DE^2+DF^2\)
nên ΔDFE vuông tại D

Bài 2:
a)
+ Xét \(\Delta MNP\) vuông tại \(N\left(gt\right)\) có:
\(MN^2+NP^2=MP^2\) (định lí Py - ta - go).
=> \(20^2+NP^2=25^2\)
=> \(NP^2=25^2-20^2\)
=> \(NP^2=625-400\)
=> \(NP^2=225\)
=> \(NP=15\left(cm\right)\) (vì \(NP>0\)).
Vậy \(NP=15\left(cm\right).\)
b)
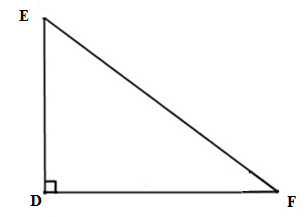
+ Xét \(\Delta DEF\) có:
\(DE^2+DF^2=10^2+24^2\)
=> \(DE^2+DF^2=100+576\)
=> \(DE^2+DF^2=676\) (1).
\(EF^2=26^2\)
=> \(EF^2=676\) (2).
Từ (1) và (2) => \(DE^2+DF^2=EF^2\left(=676\right).\)
=> \(\Delta DEF\) vuông tại \(D\) (định lí Py - ta - go đảo) (đpcm).
Chúc bạn học tốt!
Bài 1: Cho tam giác ABC có góc A=90 độ; AB<AC; phân giác BE. E∈AC. Lấy điểm H thuộc cạnh BC sao cho BH=BA.
a) Chứng minh EH ⊥ BC.
b) Chứng minh BE là đường trung trực của AH.
c) Đường thẳng EH cắt đường thẳng AB ở K. Chứng minh EK=EC.
d) Chứng minh AH//KC.
e) Gọi M là trung điểm của KC. Chứng minh ba điểm B, E, M thẳng hàng.
Help me bài này được ko!?
Vẽ hình và viết cả GT, KL hộ mình nha!

\(\text{#TNam}\)
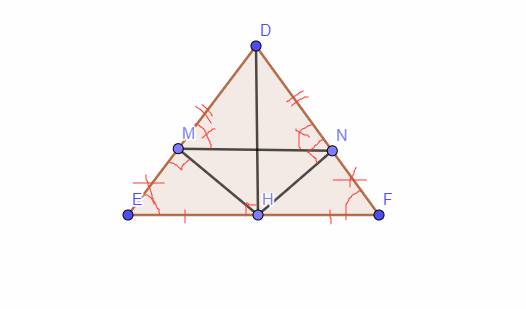
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`

1) Xét tam giác DEF có:
+ A là trung điểm của DE (gt).
+ B là trung điểm của DF (gt).
\(\Rightarrow\) AB là đường trung bình của tam giác DEF.
\(\Rightarrow\) AB // EF và AB = \(\dfrac{1}{2}\) EF (Tính chất đường trung bình trong tam giác).
2) Xét tam giác DEF vuông tại D có:
DA là đường trung tuyến (A là trung điểm của EF).
\(\Rightarrow\) DA = \(\dfrac{1}{2}\) EF (Tính chất đường trung tuyến trong tam giác vuông).
3) Xét tam giác DEF có:
+ DB là đường trung tuyến (B là trung điểm của EF).
+ DB = \(\dfrac{1}{2}\) EF (gt).
\(\Rightarrow\) Tam giác DEF vuông tại D.
