Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔJHF vuông tại H và ΔKIG vuông tại I có
HF=IG
góc JFH=góc KGI
=>ΔJHF=ΔKIG
=>HF=IG
Xét tứ giác JHKI có
JH//KI
JH=KI
=>JHKI là hình bình hành
=>HL=LI
FH+LG=IG+LQ=IL=HL

a, xét tma giác MNE và tam giác MPE có :
MN = MP và góc MNE = góc MPE do tam giác MNP cân tại M (Gt)
NE = EP do E là trđ của NP (gt)
=> tam giác MNE = tam giác MPE (c-g-c)
=> góc MEN = góc MEP (đn)
mà góc MEN + góc MEP = 180 (kb)
=> góc MEN = 90
=> MN _|_ NP và có M là trđ của PN (Gt)
=> ME là trung trực của NP (đn)
b, xét tam giác MKE và tam giác MHE có : ME chung
góc NME = góc PME do tam giác MNE = tam giác MPE (Câu a)
góc MKE = góc MHE = 90
=> tam giác MKE = tam giác MHE (ch-cgv)
=> MK = MH (đn)
=> tam giác MHK cân tại M (đn)
=> góc MKH = (180 - góc NMP) : 2 (tc)
tam giác MNP cân tại M (Gt) => góc MNP = (180 - góc NMP) : 2 (tc)
=> góc MKH = góc MNP mà 2 góc này đồng vị
=> KH // NP (đl)

a) Ta thấy :
Xét ∆ABM ta có :
AH là trung trực BM
=>∆ ABM cân tại A
Mà B = 60°
=> ∆ABM đều

a, EH _|_ BD (GT)
CD _|_ BD (GT)
=> CD // EH (tc)
=> góc HEB = góc ACB (đồng vj)
góc ACB = góc ABC do tam giác ABC cân tại A (gt)
=> góc HEB = góc ABC
xét tam giác BFE và tam giác EHB có : BE chung
góc BFE = góc EHB = 90
=> tam giác BFE = tam giác EHB (ch-gn)
b, tam giác BFE = tam giác EHB (câu a)
=> EF = BH (đn) (1)
xét tứ giác HDGE có góc EHD = góc HDG = góc DGE = 90
=> HDGE là hình chữ nhật (dh )
=> HD = EG
BH + HD = BD và (1)
=> EF + EG = BD
c,

câu a ta có : <MAE = 90
suy ra tam giác MAE là tam giác vuông :< AME + <MEA = 90 ĐỘ ( đ/lí tổng 3 góc áp dụng vào tam giác vuông )
gọi n là giao điểm của EH và CD
vì <MND =90 độ suy ra <NMD +<MPN=90độ
vì cùng phụ nhau với < m suy ra <MEA =<MDN
xét tam giác ACD và tam giác AME :
AD =AE (GT)
<MEA=<MDN (cmt)
<CAD =<MAE =90độ (do AC vuông góc với MB )
SUY RA TAM GIÁC ACD = TAM GIÁC AME(G.C.G)
:A
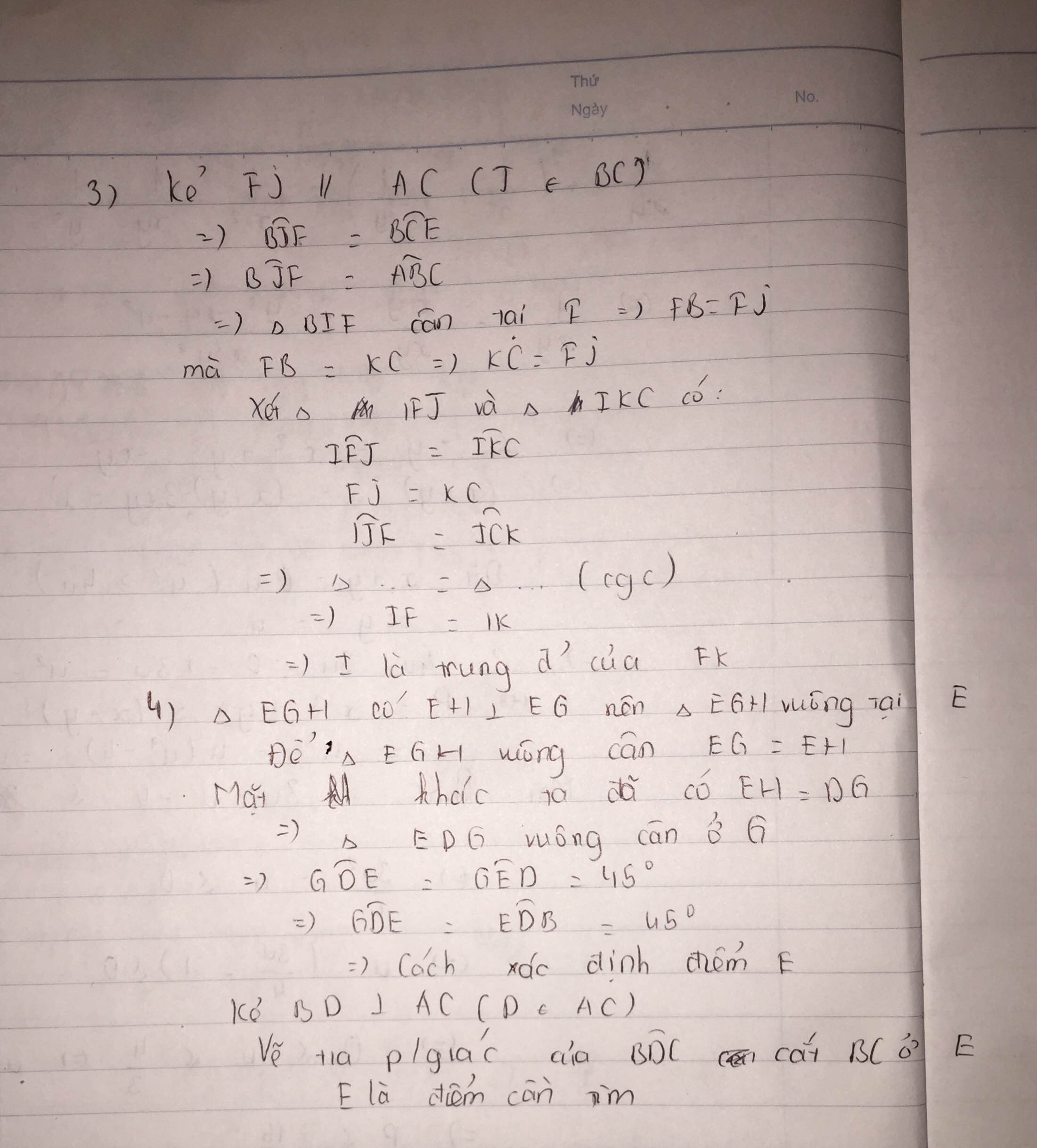



 hơi khó nhìn chút :< sorry
hơi khó nhìn chút :< sorry