Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì O thuộc đường trung trực của cạnh AB nên OA = OB. Vì ba đường trung trực của một tam giác đồng quy và do tam giác ABC cân tại A nên OA là đường trung trực của BC, do đó AO ⊥ BC. Vì tam giác ABC cân tại A nên đường trung trực AO đồng thời là đường phân giác của góc A
+) Xét ΔAOB và ΔAOC có:
OA chung
AB = AC (do tam giác ABC cân tại A)
∠OAB = ∠OAC ( Do AO là tia phân giác của góc BAC)
Do đó ΔAOB = ΔAOC ( c.g.c) suy ra ∠(AOB) = ∠(AOC) .
Do tam giác ABC cân tại A nhưng không là tam giác đều nên O không là giao điểm của ba đường phân giác của tam giác ABC. Vậy O không cách đều ba cạnh của tam giác ABC.
Đáp số (C) AO ⊥ BC.

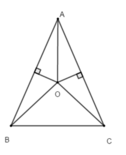
+ Vì O thuộc đường trung trực của AB nên OA = OB, do đó đáp án A sai
+ Vì ba đường trung trực của tam giác đồng quy tại một điểm nên O là giao điểm của ba đường trung trực của tam giác ABC, suy ra O thuộc đường trung trực cạnh BC
Mà AB = AC nên A thuộc đường trung trực cạnh BC
Do đó AO là đường trung trực của BC ⇒ A O ⊥ B C , nên đáp án C đúng
+ Lại có tam giác ABC cân tại A (AB = AC) có AO là trung trực nên AO cũng là phân giác của góc BAC ⇒ B A O ^ = C A O ^
Khi đó Δ B A O = Δ C A O ( c – g – c) (vì AB = AC, AO chung, B A O ^ = C A O ^ )
Suy ra A O B ^ = A O C ^ ⇒ Đáp án B sai
+ Do tam giác ABC là tam giác cân không đều nên O không phải là giao điểm của ba đường phân giác trong tam giác ABC nên O không cách đều ba cạnh của tam giác ABC, do đó đáp án D sai.
Chọn đáp án C

Vì AC là đường trung trực của BB' nên CB=CB'
=>ΔCBB' cân tại C
hay \(\widehat{BCA}=\widehat{B'CA}\)
Vì AB là đường trung trực của CC' nên BC=BC'
=>ΔBCC' cân tại B
hay \(\widehat{CBA}=\widehat{C'BA}\)
Vì AB và AC lần lượt là các đường phân giác của các góc CBB' và BCB'
và AB cắt AC tại A
nên A là điểm cách đều ba cạnh của ΔA'BC

Câu 2 (30s): Cho tam giác ABC cân tại A, trung tuyến AM cắt đường trung trực của AB tại O.
Khẳng định nào sau đây là khẳng định đúng?
A. OA = OB > OC B. OA = OB < OC
C. OA < OB = OC D. OA = OB = OC
`+` Tính chất của đường trung trực.

Điểm O cách đều AB, AC nên O thuộc tia phân giác của góc A. Mặt khác, O thuộc tia phân giác của góc B nên O là giao điểm của ba đường phân giác của tam giác ABC. Vậy (B) sai còn (A), (C), (D) đúng.
Đáp số: (B) Điểm O không nằm trên tia phân giác của góc C.

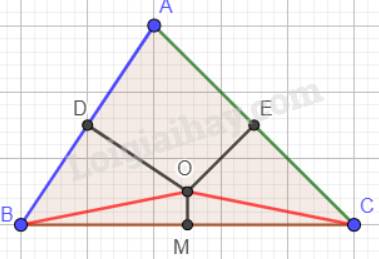
a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O. Suy ra: \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). ( tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
OB = OC;
\(\widehat {OBM} = \widehat {OCM}\);
MB = MC (M là trung điểm của đoạn thẳng BC).
Vậy \(\Delta OMB = \Delta OMC\)(c.g.c)
Do đó,\(\widehat {MOB} = \widehat {MOC}\) ( 2 góc tương ứng).

Chọn C