Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

\(AB^2+AC^2=BC^2=25\Rightarrow5AC^2=25\Leftrightarrow AC=\sqrt{5}\left(cm\right)\Rightarrow AB=2\sqrt{5}\left(cm\right)\)\(CH=\dfrac{AC^2}{BC}=1\left(cm\right)\Rightarrow BH=5-1=4\left(cm\right)\\ AH=\dfrac{AB.AC}{BC}=2\\ AI=\dfrac{1}{3}AH=\dfrac{2}{3};HI=\dfrac{2}{3}AH=\dfrac{4}{3}\\ CD\text{//}AH\Rightarrow CD\text{//}HI\Rightarrow\dfrac{HI}{CD}=\dfrac{BH}{BC}=\dfrac{4}{5}\\ \Rightarrow CD=\dfrac{5}{4}HI=\dfrac{5}{4}\cdot\dfrac{4}{3}=\dfrac{5}{3}\\ \Rightarrow S_{AHCD}=\dfrac{1}{2}\cdot HC\cdot\left(AH+CD\right)=\dfrac{1}{2}\cdot1\cdot\left(2+\dfrac{5}{3}\right)=\dfrac{11}{6}\left(cm^2\right)\left(AH\text{//}CD\text{ nên }AHCD\text{ là hình thang}\right)\)

a:
ΔABC cân tại A
=>góc ABC=góc ACB=(180-34)/2=146/2=73 độ
Xét ΔABC có BC/sinA=AB/sinC=AC/sinB=2R
=>BC/sin34=8/sin73
=>\(BC\simeq4,68\left(cm\right)\)
b: Xét ΔADC có \(cosCAD=\dfrac{AC^2+AD^2-CD^2}{2\cdot AC\cdot AD}\)
=>\(8^2+10.6^2-CD^2=2\cdot8\cdot10.6\cdot cos42\)
=>\(CD\simeq7,09\left(cm\right)\)
Xét ΔACD có
\(\dfrac{AC}{sinADC}=\dfrac{CD}{sinCAD}\)
=>8/sinADC=7,09/sin42
=>\(sinADC\simeq0,76\)
=>\(\widehat{ADC}\simeq49^0\)
c:
góc DAB=góc DAC+góc BAC
=42+34
=76 độ
Kẻ BH vuông góc AD
=>BH=d(B;AD)
Xét ΔBHA vuông tại H có
sinHAB=BH/BA
=>BH/8=sin76
=>\(BH\simeq7,76\left(cm\right)\)

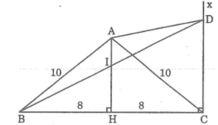
Áp dụng định lí Pi-ta-go vào tam giác vuông ABH ta có:
A B 2 = A H 2 + B H 2 ⇒ A H 2 = A B 2 - B H 2 = 10 2 - 8 2 = 36
Suy ra: AH = 6 (cm)
![]()
Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)
Vì IH ⊥ BC và DC ⊥ BC nên IH // DC (1)
Mặt khác: BH = HC (gt) (2)
Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD


Xét \(\Delta\)ABC cân tại A có :
AH là đường cao
\(\Rightarrow\)AH là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
\(\Rightarrow\)BH = HC =\(\dfrac{BC}{2}\)\(\dfrac{16}{2}=8\)
Xét \(\Delta\)AHB vuông tại H có:
\(\cos\)B=\(\dfrac{BH}{AB}=\dfrac{8}{10}\)=0.8
\(\Rightarrow\Lambda B\approx37\)độ
Ta có : góc B = góc C (Tam giác ABC cân tại A)
Mà góc B\(\approx37\)độ
\(\Rightarrow\)góc C\(\approx\)37 độ
b, Xét \(\Delta\)ABC có :
góc BAC+gócACB+góc ABC=180
\(\Rightarrow\)góc BAC=106 độ
Xét \(\Delta\)AHB vuông tại H có :
\(AB^2=AH^2+HB^2\Rightarrow AH=6\)
Ta có \(AI=\dfrac{1}{3}AH\Rightarrow HI=\dfrac{2}{3}AH\)
\(\Rightarrow\)HI=4cm
Xét tam giác BDC có
\(HI\) song song CD
\(\Rightarrow\dfrac{HI}{CD}=\dfrac{BH}{CH}=\dfrac{8}{16}=\dfrac{1}{2}\)
\(CD=8cm\)
Xét tứ giác AHCD có :
AH song somg CD
\(\Rightarrow\)AHCD là hình thang
Diện tích hình thang AHCD là :
\(\dfrac{1}{2}\left(6+8\right)\times8=56cm^2\)
Diện tích AHB là :
\(\dfrac{1}{2}\times6\times8=24cm^2\)
Diện tích tứ giác ABCD là
\(56+24=80cm^2\)

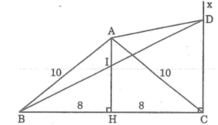
Ta có: AH ⊥ BC, suy ra: HB = HC = BC/2 = 8 (cm)
Trong tam giác vuông ABH, ta có:



Xét tam giác AHD vuông tại H
=> \(\sin\widehat{AHD}=\frac{AH}{DA}=\frac{3}{DA}\)
=> \(DA=\frac{3}{\sin65^o}\)
Kẻ BK vuông với DA tại K
=> Khoảng cách từ B đến AD =BK
Xét tứ giác ACBK: có
CB// AK ( CB// AD)
BK // AC ( cùng vuông với AD
=> ACBK là hình bình hành
=> BK=AC
Xét tam giác ACD có:
\(\tan\widehat{AHC}=\frac{AC}{DA}\Rightarrow AC=\tan\widehat{AHC}.AD=\tan65^o.\frac{3}{\sin65^o}=\frac{3}{\cos65^o}\)
=> KHoảng cách từ B đến AD bằng \(\frac{3}{\cos65^o}\)
Dễ dàng cm đc ADCB là hình bình hành:
=> AK=AD=BC=> DK=2. AD=\(\frac{6}{\sin65^o}\)
Xét tam giác KDB vuông tại K có DK=\(\frac{6}{\sin65^o}\), BK=\(\frac{3}{\cos65^o}\). Sử dụng định lí pitago để tìm DB
Diện tích tam giác ABD= 1/2 . BK .AD . Thay vào tính đẻ tìm kết quả
Ủa sao lúc nãy đề khác mà nhỉ ???
Kẻ BK vuông góc với AD
Xét \(\Delta ADC\left(\widehat{A}=90^o\right):\widehat{ADC}=65^o\Rightarrow\widehat{ACD}=25^o\)
Khi đó \(CA=\frac{AH}{sin\widehat{C}}=\frac{3}{sin25^o}\)
Dễ thấy BCAK là hình chữ nhật => \(BK=AC=\frac{3}{sin25^o}\)(cm)
và BC = AK
=> DA = AK (=BC)
=> DK = 2.DA
Ta có \(DA=\frac{AH}{sin\widehat{CDA}}=\frac{3}{sin25^o}\)(cm)
\(\Rightarrow DK=2DA=\frac{6}{sin25^o}\)(cm)
Áp dụng định lí Pytago vào tam giác BKD vuông tại K có
\(BK^2+KD^2=BD^2\)
\(\Leftrightarrow\left(\frac{3}{sin25^o}\right)^2+\left(\frac{6}{sin25^o}\right)^2=BD^2\)
\(\Leftrightarrow BD^2=\frac{45}{sin^225^o}\)
\(\Leftrightarrow BD=\frac{3\sqrt{5}}{sin25^o}\)(cm)
Ta có \(S_{ABD}=S_{BKD}-S_{BAK}\)
\(=\frac{BK.KD}{2}-\frac{AK.BK}{2}\)
\(=\frac{BK}{2}\left(KD-AK\right)\)
\(=\frac{BK.AD}{2}\)
\(=\frac{\frac{3}{sin25^o}.\frac{3}{sin25^o}}{2}\)
\(=\frac{18}{sin25^o}\left(cm^2\right)\)
Tính sai ở đâu tự sửa nhá :V