K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
11 tháng 12 2019
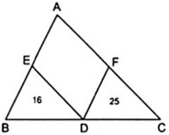
Đặt S A B C = S . Vì DE//AC nên Δ BED ∼ Δ BAC
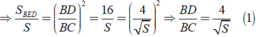
Lại có DF//AB nên Δ CDF ∼ Δ CBA
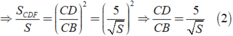
Cộng theo vế của đẳng thức ( 1 ) và ( 2 ) ta được:
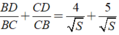
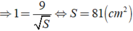
Vậy diện tích của tam giác ABC là 81 c m 2

3 tháng 2 2022
a: Xét tứ giác AFME có
MF//AE
ME//AF
Do đó: AFME là hình bình hành
mà \(\widehat{FAE}=90^0\)
nên AFME là hình chữ nhật
b: Để AFME là hình vuông thì AM là tia phân giác của góc FAE
Vậy: Khi M là chân đường phân giác kẻ từ A đến BC thì AFME là hình vuông

a. Do ME // AC nên \(\frac{ME}{AC}=\frac{BM}{BC}\); MF // AB nên \(\frac{MF}{AB}=\frac{MC}{BC}\)
Từ đó suy ra \(\frac{ME}{AC}+\frac{MF}{AB}=\frac{BM+MC}{BC}=1\) không đổi.
b. Gọi \(\frac{ME}{AC}=t\Rightarrow\frac{MF}{AB}=1-t\Rightarrow S_{ABC}=\frac{a^2}{t^2}=\frac{b^2}{\left(1-t\right)^2}\)
\(\Rightarrow\frac{a}{t}=\frac{b}{1-t}\Rightarrow a\left(1-t\right)=bt\Rightarrow t=\frac{a}{a+b}\Rightarrow t^2=\frac{a^2}{\left(a+b\right)^2}\Rightarrow S_{ABC}=\frac{a^2}{t^2}=\left(a+b\right)^2.\)
c. \(S_{AEMF}=S_{ABC}-S_{BME}-S_{CMF}=\left(a+b\right)^2-a^2-b^2\)
\(=2ab\le a^2+b^2\)
Dấu bằng xảy ra khi a = b, tức là M là trung điểm BC.