Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta EBCcó:BE=BC\left(gt\right)\)
\(\Rightarrow\Delta EBC\) cân tại B
\(\Rightarrow\) góc E = góc C
Ta có : góc ABD + góc DBC + góc CBE = 1800 (kề bù)
\(\Rightarrow\) góc CBE = 1800 - ( góc ABD + góc DBC)
Và ta lại có: góc E + góc CBE + góc C = 1800 (tổng 3 góc trong tam giác EBC)
\(\Rightarrow\) góc CBE = 1800 - ( góc E + góc C)
Mà : góc ABD = góc DBC ( vì BD là tia phân giác của góc ABC)
góc E = C ( cmt )
\(\Rightarrow\) góc DBC = góc C
Mà : 2 góc này nằm ở vị trí so le trong
\(\Rightarrow BDsong^2EC\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: AD=ED
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
c: Ta có: ΔADF=ΔEDC
nên DF=DC và AF=EC
Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BC=BF
hay B nằm trên đường trung trực của CF(1)
Ta có: DF=DC
nên D nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra BD\(\perp\)CF

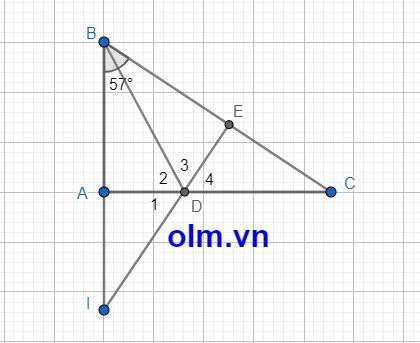
Xét tam giác ABD và tam giác EBD có
\(\widehat{ABD}\) = \(\widehat{EBD}\) (gt)
AB = BE (gt)
BD chung
⇒\(\Delta\)ABD = \(\Delta\) EBD (c-g-c)
⇒AD = DE
⇒ \(\widehat{BAD}\) = \(\widehat{BED}\) = 900
\(\widehat{DEC}\) = 1800 - 900 = 900
Xét tam giác ADI và tam giác EDC có:
\(\widehat{DAI}\) = \(\widehat{DEC}\) = 900 (cmt)
AD = DE (cmt)
AI = EC (gt)
⇒ \(\Delta\)ADI = \(\Delta\)EDC (c-g-c)
⇒ D1 = D4
Mà D2 + D3 + D4 = 1800
⇒ D1 + D2 + D3 = 1800
⇒ \(\widehat{IDE}\) = 1800
⇒ I;D;E thẳng hàng (đpcm)
 Do BD là tia phân giác của ∠ABC (gt)
Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ DE ⊥ BC
Do AI = EC (gt)
AB = BE (gt)
⇒ BI = AI + AB = BE + EC = BC
∆BCI có:
BI = BC (cmt)
⇒ ∆BCI cân tại B
Mà BD là tia phân giác của ∠ABC
⇒ BD là tia phân giác của ∠IBC
⇒ BD là đường cao của ∆BCI
Lại có:
CA ⊥ AB (∆ABC vuông tại A)
CA ⊥ BI
⇒ CA là đường cao thứ hai của ∆BCI
⇒ ID là đường cao thứ ba của ∆BCI
⇒ ID ⊥ BC
Mà DE ⊥ BC (cmt)
⇒ I, D, E thẳng hàng
Vẽ hình đi mình nhờ bạn đấy