Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AI là đường cao ứng với cạnh huyền BD, ta được:
\(BI\cdot BD=AB^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BI\cdot BD=BH\cdot BC\)

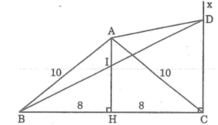
Ta có: AH ⊥ BC, suy ra: HB = HC = BC/2 = 8 (cm)
Trong tam giác vuông ABH, ta có:
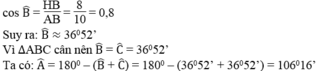

Áp dụng định lí Pi-ta-go vào tam giác vuông ABH ta có:
A B 2 = A H 2 + B H 2 ⇒ A H 2 = A B 2 - B H 2 = 10 2 - 8 2 = 36
Suy ra: AH = 6 (cm)
![]()
Suy ra: IH = AH – AI = 6 – 2 = 4 (cm)
Vì IH ⊥ BC và DC ⊥ BC nên IH // DC (1)
Mặt khác: BH = HC (gt) (2)
Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD


a: góc ADB=góc ABD=45 độ
góc AKH=góc KAH=45 độ
=>góc ADB=góc AKB
=>ADKB nội tiép
b: ADKB là tứ giác nội tiếp
=>góc AKD=góc ABD=45 độ