Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD vuông tại D và ΔCBE vuông tại E có
góc B chung
=>ΔABD đồng dạng với ΔCBE
b:
ΔABC cân tại A có AD là đường cao
nên D là trung điểm của BC
=>DB=DC=12/2=6cm
=>AD=8cm
ΔABD đồng dạng với ΔCBE
=>BE/BD=AB/CB=AD/CE
=>BE/6=10/12=8/CE
=>BE=5cm; CE=12*8/10=9,6cm
c: Xét ΔCDH vuông tại D và ΔCEB vuông tại E có
góc HCD chung
=>ΔCDH đồng dạng với ΔCEB
=>HD/EB=CD/CE
=>HD/5=6/9,6=5/8
=>HD=25/8cm

Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=8cm\)
Vì BE là pg \(\dfrac{AB}{BC}=\dfrac{AE}{EC}\Rightarrow\dfrac{EC}{BC}=\dfrac{AE}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{EC}{BC}=\dfrac{AE}{AB}=\dfrac{AC}{AB+BC}=\dfrac{8}{16}=\dfrac{1}{2}\Rightarrow EC=5cm;AE=3cm\)

xét ΔABC có AD là đường phân giác
->\(\dfrac{AB}{BO}=\dfrac{AC}{OC}\)
áp dụng dãy tỉ số bằng nhau ta có
\(\dfrac{AB}{BO}=\dfrac{AC}{OC}=\dfrac{AB+AC}{BO+DO}=\dfrac{AC+AB}{BC}hay\dfrac{6}{BO}=\dfrac{10}{OC}=\dfrac{10+6}{8}=2\)
suy ra: \(BO=\dfrac{6}{2}=3\left(cm\right)\)
\(CO=\dfrac{10}{2}=5\left(cm\right)\)

a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
Suy ra: \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AC^2=CH\cdot BC\)(đpcm)

a: \(BC=\sqrt{18^2+24^2}=30\left(mm\right)\)=3(cm)
Xét ΔACB có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=2,4/8=0,3
=>AD=0,9cm; CD=1,5cm
b: Xét ΔCED và ΔCAB có
CE/CA=CD/CB
góc C chung
=>ΔCED đồng dạng với ΔCAB
=>góc CED=góc CAB=90 độ
d: ΔCED đồng dạng với ΔCAB
=>ED/AB=CE/CA
=>ED/1,8=1,2/2,4
=>ED=0,9cm
c: ΔCED đồng dạng với ΔCAB
=>\(\dfrac{S_{CED}}{S_{CAB}}=\left(\dfrac{CE}{CA}\right)^2=\dfrac{1}{4}\)

a, Xét hai tam giác ABM và CBM có:
\(\widehat{B}\) là góc chung
\(\dfrac{AB}{BC}=\dfrac{NB}{MB}\) ( Do tam giác ABC cân tại B)
=> tam giác ABM đồng dạng tam giác CBM (c.g.c)
b, Do tam giác ABM∼ tam giác CBN nên ta có tỉ lệ:
\(\dfrac{BM}{BC}=\dfrac{BN}{AB}\) => MN // AC (đpcm)

a: \(CB=\sqrt{18^2+24^2}=30\left(mm\right)\)
Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5=24/8=3mm
=>AD=9mm; CD=15mm
b: CA=24mm; CB=30mm; CE=12mm; CD=15mm
=>CA/CE=CB/CD
=>ΔCAB đồng dạng với ΔCED
=>góc CED=90 độ

\(AC=AB=6\)
Áp dụng định lý phân giác:
\(\dfrac{AD}{AB}=\dfrac{DC}{BC}\Leftrightarrow\dfrac{AD}{6}=\dfrac{6-AD}{10}\)
\(\Leftrightarrow10AD=36-6AD\Rightarrow AD=\dfrac{9}{4}\) (cm)
\(\Rightarrow DC=AC-AD=\dfrac{15}{4}\) (cm)

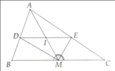
Xét ΔABC có BE là phân giác
nên AB/AE=BC/CE=2
=>AB=2AE
=>tan ABE=1/2
1+tan^2ABE=1/cos^2(ABE)
=>1/cos^2ABE=1+1/4=5/4
=>cos^2ABE=4/5
=>cos ABE=2/căn 5
cos ABC=cos (2*ABE)
\(=2\cdot\left(\dfrac{2}{\sqrt{5}}\right)^2-1=\dfrac{3}{5}\)
=>AB/BC=3/5
=>AB=6cm
=>AC=8cm