Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

( Thông cảm hình bị lệch )
a) + Xét \(\Delta ABC\)và \(\Delta DMC\)có :
AM = DM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)( vì là hai góc đối đỉnh ) => \(\Delta AMB=\Delta DMC\)
MB = MC ( AM là trung tuyến của \(\Delta ABC\))
=> \(\widehat{B}=\widehat{MCD}\)( hai góc tương ứng )
=> DC // AB ( có hai góc so le trong = )
Mà AB \(\perp\)AC ( Vì \(\Delta ABC\)vuông tại A)
=> DC _|_ AC
+ Xét \(\Delta BEC\)có :
M là trung điểm của cạnh BC ( Vì AM là trung tuyến của ABC )
=> EM là trung tuyến
A là trung điểm của BE ( Vì EA = AB ) => CA là trung tuyến
Mà EM cắt AC tại N => N là trọng tâm của \(\Delta ABC\)
\(\Rightarrow NC=\frac{2}{3}CA\Rightarrow NC=2NA\)
+ Ta có \(\Delta AMB=\Delta DMC\Rightarrow AB=CD\)
Xét \(\Delta ACD\)có :
CD + AC > AD ( bđt tam giác ) . Mà CD = AB ; AD = 2AM
=> \(AB+AC>2AM\Leftrightarrow\frac{AB+AC}{2}>AM\)(1)
+ Xét \(\Delta AMB\)có : AM > AB - BM
\(\Delta AMC\)có : AM > AC - CM
=> 2AM > AB + AC - BM - CM
<=> 2AM > AB + AC - (BM +CM )
<=> 2AM > AB + AC - BC
<=> AM > \(\frac{AB+AC-BC}{2}\)(2)
Từ (1), (2) => Điều cần cm trên đề bài .

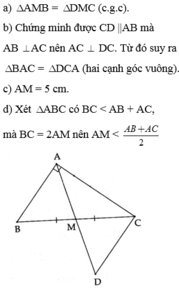
a ) + ΔAMB = ΔDMC ( c.g.c )
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\)
=> AB // CD => CD ⊥ AC
b) + Xét ΔBEC có 2 đg trung tuyến EM và CA cắt nhau tại N
=> N là trọng tâm ΔBEC
=> NC = 2 NA
c) Xét ΔABM theo bất đẳng thức tam giác :
\(AM>AB-BM\)
+ Tương tự ta cm đc : \(AM>AC-CM\)
Do đó : 2AM > AB + AC - ( BM + CM )
=> \(2AM>AB+AC-BC\)
\(\Rightarrow\frac{AB+AC-BC}{2}< AM\) (1)
+ ΔAMB = ΔDMC ( c.g.c )
=> AB = CD
+ Xét ΔACD theo bđt tam giác :
\(AD< AC+CD\)
\(\Rightarrow2AM< AC+AB\)
\(\Rightarrow AM< \frac{AB+AC}{2}\) (2)
+ Từ (1) và (2) suy ra : \(\frac{AB+AC-BC}{2}< AM< \frac{AB+AC}{2}\)

\(a)\)
Vì \(AM\)là đường trung tuyến
\(\rightarrow BM=CM\)
Xét \(\Delta AMB\)và \(\Delta DMC\)ta có:
\(\hept{\begin{cases}BM=CM\left(cmt\right)\\MD=MA\left(GT\right)\\\widehat{BMA}=\widehat{DMC}\end{cases}}\)
\(\rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
\(b)\)
Vì \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\rightarrow\hept{\begin{cases}\widehat{ABM}=\widehat{MCD}\\AB=CD\end{cases}}\)
Mà hai góc này ở vị trí so le trong
\(\rightarrow AB//CD\)
Mà \(AB\perp AC\)( vì \(\Delta ABC\)vuông tại \(A\))
\(\rightarrow CD\perp AC\)
Xét \(\Delta ABC\)và \(DCM\)ta có:
\(\hept{\begin{cases}AB=CD\left(cmt\right)\left(cmt\right)\\ACchung\\\widehat{BAC}=\widehat{DCA}=90^o\end{cases}}\)
\(\rightarrow\Delta ABC=\Delta DMC\left(c.g.c\right)\)
\(c)\)
Ta có: \(AB=DC=6cm\)
Xét \(\Delta DCA\)vuông tại \(C\)ta có:
\(DC^2+AC^2=AD^2\)
\(\rightarrow AD^2=6^2+8^2\)
\(\rightarrow AD^2=10^2\)
\(\rightarrow AD=10cm\)
Mà \(MD=MA\)
\(\rightarrow M\)là trung điểm của \(AD\)
\(\rightarrow AM=\frac{1}{2}AD=\frac{1}{2}.10=5cm\)
\(d)\)
Giả sử: \(AM< \frac{AB+AC}{2}\)
Ta có: \(\frac{AB+AC}{2}=\frac{6+8}{2}=\frac{14}{2}=7cm\)
Mà \(AM=5cm\)
\(\rightarrow5cm< 7cm\)
\(\rightarrow AM< \frac{AB+AC}{2}\)

a) Xét tam giác CMA và tam giác BMD có :
\(\hept{\begin{cases}MC=MB\\AM=MD\\\widehat{AMC}=\widehat{BMD}\end{cases}\Rightarrow\Delta CMA=\Delta BMD}\)
=> \(\hept{\begin{cases}AC=BD\\\widehat{BDM}=\widehat{ACM}\end{cases}\Rightarrow BD//AC}\)
=> ACBD là hình bình hành
=> \(\hept{\begin{cases}AB=CD\\AB//CD\end{cases}}\)=> đpcm
b) Xét tam giác ABC và tam giác CDA có :
\(\hept{\begin{cases}AB=CD\\\widehat{CAB}=\widehat{ACD}=90^∗\end{cases}\Rightarrow\Delta ABC=\Delta CDA}\)( Lưu ý : Vì không có dấu kí hiệu " độ " nên em dùng tạm dấu *)
Chung AC
=> AD=BC
=> \(AM=\frac{1}{2}.AD=\frac{1}{2}.BC\)=> đpcm
c) Xét tam giác ABC có :
M là trung điểm BC
A là trung điểm CE
Từ 2 điều trên =>AM là đường trung bình => AM//BE ( đpcm )
e) AM //BE => AD // BE
Tam giác CBE có BA vừa là đường cac ,vừa là trung tuyến => tam giác CBE cân ở B
=> \(\hept{\begin{cases}BC=BE\\AD=BC\end{cases}\Rightarrow AD=EB}\)
Mà AD//BE => ABDE là hình bình hành => AB cắt DE ở trung điểm
=> E,O , D thẳng hàng => đpcm

tu ve hinh :
a, xet tamgiac MBA va tamgiac MDC co :
goc BMA = goc DMC (doi dinh)
BM = CM do M la trung diem cua BC (GT)
MA = MD (GT)
=> tamgiac MBA = tamgiac MDC (c - g - c)
=> AB = DC (dn)
tamgiac MBA = tamgiac MDC => goc CDM = goc MAB ma 2 goc nay slt
=> AB // CD (dh)
b, co tamgiac ABC vuong tai A => AB | AC (dn) ; AB // DC (cau a)
=> AC | DC (dl) => tamgiac ACD vuong tai C (dn)
tamgiac MBA = tamgiac MDC => AB = CD (dn)
goc BAC = goc DCA = 90o do tamgiac ABC vuong tai A va tamgiac DCA vuong tai C
xet tamgiac ACB va tamgiac CAD co AC chung
=> tamgiac ACB = tamgiac CAD (2cgv)
=> BC = AD (dn)
M la trung diem cua BC => M la trung diem cua AD => AM = AD/2 (tc)
=> AM = BC/2

có qá thừa không khi trả lời vào câu đã có 2 người làm rồi vag cách làm thì chắt lọc lại từ hai bài??
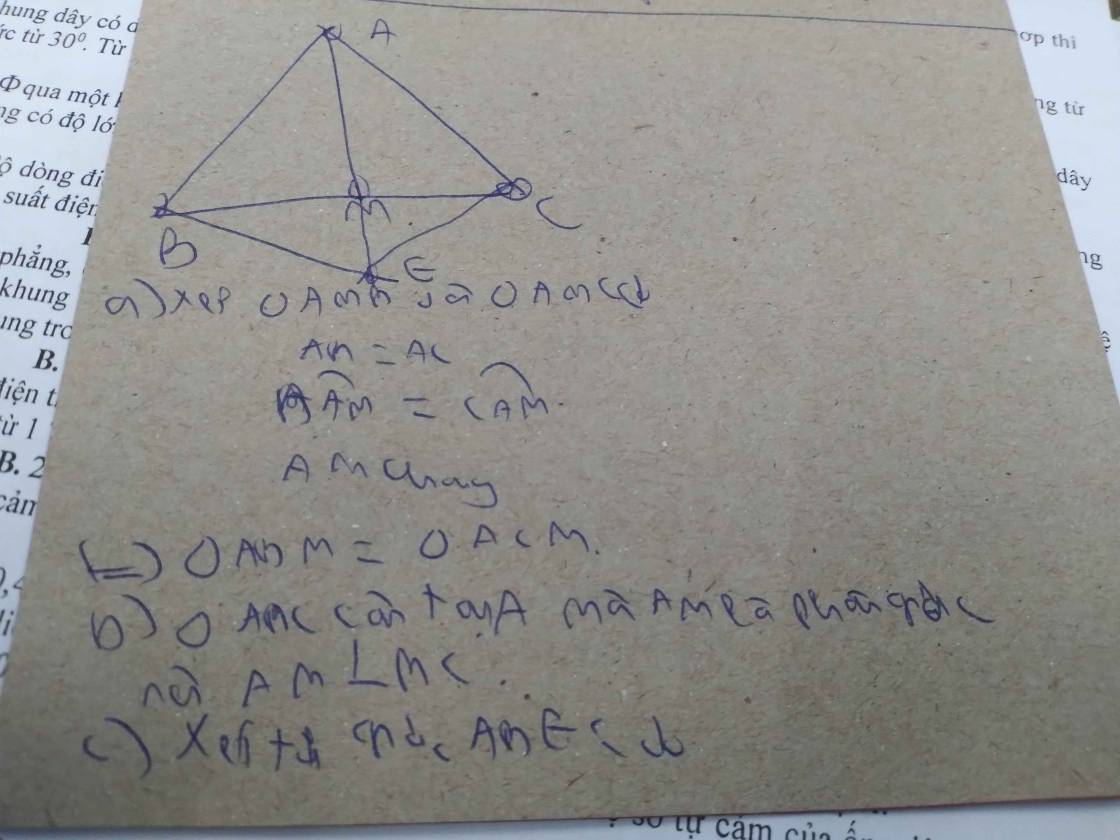
1)Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\(\widehat{BMA}=\widehat{DMC}\) (đđ)
BM = MC (gt)
AM = DM (gt)
⇒ \(\Delta AMB\) = \(\Delta DMC\) (c.g.c)
⇒ \(\widehat{ABM}=\widehat{BCM}\) (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí So le trong nên:
⇒ AB // DC
Ta lại có: AB ⊥ AC
⇒ DC ⊥ AC
2)
Ta có E ∈ tia đối của tia AB mà EA = EB
⇒ A là trung điểm của EB
Xét ΔBCE có 2 trung tuyến EM và CA cắt nhau tại N
⇒ N là trọng tâm của ΔBCE
⇒ NC = 2NA (ĐPCM)
3)
Từ ΔABM và ΔACM có:
\(\left\{{}\begin{matrix}AB< BM+AM\\AC< AM+MC\end{matrix}\right.\)
⇒ AB + AC < BM + AM + AM + MC
⇒ AB + AC < BC + 2AM
⇒ 2 AM < AB + AC - BC
⇒ AM > \(\frac{\text{AB + AC - BC}}{2}\) (1)
Ta có: ΔAMB = ΔDMC (câu 1)
⇒ AB = DC
Xét trong ΔACD có:
AD < DC + CA
⇔ 2AM < AB + AC
⇒ AM < \(\frac{\text{AB + AC}}{2}\) (2)
Từ (1) và (2), ta có:
\(\frac{\text{AB + AC - BC}}{2}\) < AM < \(\frac{\text{AB + AC}}{2}\) (ĐPCM)