Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét Δ BIC có:
BA là đường cao
BA là đường trung tuyến
⇒ ΔBIC cân tại B
Ta có: BAI=BAC(c-g-c)
Ta có: Tam giác BIC cân tại B
Mà BA là đường cao
⇒BA là đường phân giác của góc HBK
b):
Ta có ΔABK=CBA( ch-gn)=>AB^2=BK.BC(1)
Ta có ΔABH=IBA( ch-gn)=>AB^2=BH.BI(2)
(1)(2)=>BK.BC=BH.BI=>HK//IC ( định lý Ta-lét)
c):
Gọi E là giao điểm của HK&BA
Có Tam giác BHK cân ( BE là đường cao, phân giác)⇒BH=BK
Ta có BA là đường trung trực của HK⇒HA=AK
Có tam giác vg BHN=BKM (gn-cgv⇒HN=KM
⇒HA+AN=AK+AM
⇒AN=AM
⇒Δ AMN cân tại A

Có gì khong hiểu hỏi lại cj nhé:
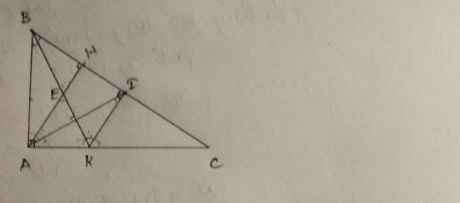
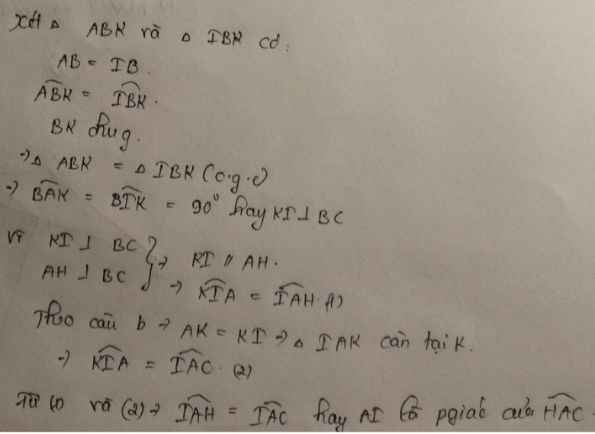
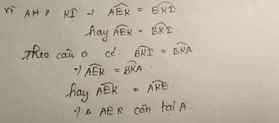
a, b ,c lần lượt từ trên xuống.

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AK=AH
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
e: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao
a) Xét \(\Delta BAI\)và \(\Delta BAC\)có :
AB : cạnh chung
\(\widehat{BAI}=\widehat{BAC}\left(=90^0\right)\)
AC = AI ( gt )
\(\Rightarrow\Delta BAI=\Delta BAC\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{ABC}\)( do 2 tam giác = nhau )
Mà \(\widehat{ABI}+\widehat{BAH}=90^0\)( tổng 3 góc = 1800 mà có 1 góc = 900 ( do AH\(\perp\)BI ) nên tổng 2 góc còn lại = 900 )
\(\Rightarrow\widehat{ABC}+\widehat{BAK}=90^0\)
\(\Rightarrow\widehat{BAH}=\widehat{BAK}\)
=> BA là đường phân giác của \(\widehat{HBK}\)
b) Ta có tam giác vuông ABK = CBA ( ch-gn ) => AB2 = BK . BC (1)
Ta có tam giác vuông ABH = IBA ( ch-gn ) => AB2 = BH . BI (2)
Từ (1) và (2) => BK . BC = BH . BI => HK // IC ( theo định lí Ta-let )
c) Gọi E là giao điểm của HK và BA
Có tam giác BHK cân ( BE là đường cao, phân giác ) => BH = BK
Ta có BA là đường trung trực của HK => HA = KA
Có tam giác vuông BHN = BKM ( gn-cgv ) => HN = KM
=> HA + AN = AK + AM => AN = AM => Tam giác AMN cân tại A