Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

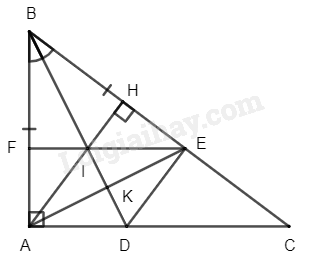
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:
\(BA = BE\) (gt)
\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)
\(BD\) chung
Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)
b) Vì \(\Delta ABD = \Delta EBD\) (cmt)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DE \bot BC\)
Mà \(AH \bot BC\) (gt)
Suy ra \(AH\) // \(DE\)
Suy ra \(ADEH\) là hình thang
Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)
Suy ra \(ADEH\) là hình thang vuông
c)
Gọi \(K\) là giao điểm của \(AE\) và \(AD\)
Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)
Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )
Suy ra \(BK\) cũng là đường cao
Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)
Suy ra \(I\) là trực tâm của \(\Delta ABE\)
Suy ra \(EF \bot AB\)
Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))
Suy ra \(AC\) // \(EF\)
Suy ra \(ACEF\) là hình thang
Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)
Suy ra \(ACEF\) là hình thang vuông

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=góc BAD=90 độ
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
Do đó: ΔBEF=ΔBAC
=>BF=BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
BA=BE
=>B nằm trên trung trực của AE(1)
DA=DE
=>D nằm trên trung trực của AE(2)
Từ (1), (2) suy ra BD là đường trung trực của AE
=>BD vuông góc AE

Sửa đề: ΔABC cân tại A
a:ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
=>AD vuông góc BC
b: Xét ΔAFI và ΔAEI có
AF=AE
góc FAI=góc EAI
AI chung
=>ΔAFI=ΔAEI
=>góc AFI=góc AEI
=>FI vuông góc AB
c: Xét ΔABC có
BE,AD là đường cao
BE cắt AD tại I
=>I là trực tâm
=>CI vuông góc AB
=>C,I,F thẳng hàng

Bài 3:
a: Xét tứ giác ABNC có
M là trung điểm chung của AN và BC
=>ABNC là hình bình hành
Hình bình hành ABNC có AB=AC
nên ABNC là hình thoi
b: Ta có:ABNC là hình thoi
=>AB//NC
mà D\(\in\)NC
nên AB//CD
Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
=>AD=BC
c: Xét ΔADN vuông tại A có \(DN^2=AD^2+AN^2\)
=>\(DN^2=9^2+12^2=225\)
=>\(DN=\sqrt{225}=15\left(cm\right)\)
Xét ΔAND vuông tại A có AH là đường cao
nên \(AH\cdot ND=AN\cdot AD\)
=>\(AH\cdot15=9\cdot12=108\)
=>AH=108/15=7,2(cm)
Bài 4:
a: Xét tứ giác AEMN có
AE//MN
AN//ME
Do đó: AEMN là hình bình hành
Hình bình hành AEMN có AM là phân giác của góc EAN
nên AEMN là hình thoi
b: Ta có; ΔABC cân tại A
mà AM là đường phân giác
nên AM\(\perp\)BC và M là trung điểm của BC
Xét ΔABC có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
Xét ΔABC có
M,N lần lượt là trung điểm của BC,CA
=>MN là đường trung bình của ΔABC
=>MN//AB và MN=AB/2
Ta có: MN=AB/2
MN=MD/2
Do đó: AB=MD
Xét tứ giác ABMD có
DM//AB
DM=AB
Do đó: ABMD là hình bình hành
c: Xét tứ giác AMCD có
N là trung điểm chung của AC và MD
=>AMCD là hình bình hành
Hình bình hành AMCD có \(\widehat{AMC}=90^0\)
nên AMCD là hình chữ nhật
d: Để ADCM là hình vuông thì AM=CM
=>AM=BC/2
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Để mình làm cho
xét tam giác ABD và tam giác EBD có
BD chung
ABD=EBD( vì BD là phân giác )
BAD=BED=90 độ
suy ra tam giác ABD=tam giác EBD ( cạnh huyền - góc nhọn)
vậy tam giác ABD = tam giác EBD
b vì tam giác ABD =tam giác EBD ( cm câu a)
suy ra AB = EB ( 2 cạnh tương ứng)
suy ra tam giác ABE cân tại b
mà góc B = 60 độ
suy ra tam giác ABE đều
Vậy tam giác ABE đều
c từ từ mình đang nghĩ
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔABD=ΔEBD)
\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADM=ΔEDC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AM=EC(Hai cạnh tương ứng)
c) Xét ΔBAE có BA=BE(gt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Suy ra: \(\widehat{BAE}=\widehat{BEA}\)(hai góc ở đáy)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
và \(\widehat{BEA}+\widehat{AEC}=180^0\)(hai góc kề bù)
nên \(\widehat{AEC}=\widehat{EAM}\)