Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
a. Tứ giác $AEHF$ có 3 góc vuông: $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hình chữ nhật.
b. Vì $I, H$ đối xứng với nhau qua $E$ nên $E$ là trung điểm của $IH$
Xét tam giác $AIE$ và $AHE$ có:
$AE$ chung
$IE=EH$ (do $E$ là trung điểm $IH$)
$\widehat{AEI}=\widehat{AEH}=90^0$
$\Rightarrow \triangle AIE=\triangle AHE$ (c.g.c)
$\Rightarrow \widehat{IAE}=\widehat{HAE}(1)$
Tương tự: $\triangle AHF=\triangle AKF$ (c.g.c)
$\Rightarrow \widehat{KAF}=\widehat{HAF}(2)$
Từ $(1); (2)\Rightarrow \widehat{IAE}+\widehat{KAF}+\widehat{BAC}=\widehat{HAE}+\widehat{HAF}+\widehat{BAC}$
Hay $\widehat{IAK}=\widehat{BAC}+\widehat{BAC}=90^0+90^0=180^0$
$\Rightarrow I,A,K$ thẳng hàng.
a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trun điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC; DM = 1/2AC
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành)
c) Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành ( D/h 5 )
mà AB vuông góc EM
=> hbh AEBM là hình thoi ( D/h 3 )
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền)
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm)
Chu vi hình thoi AEBM:
2,5 . 4 =10 (cm)
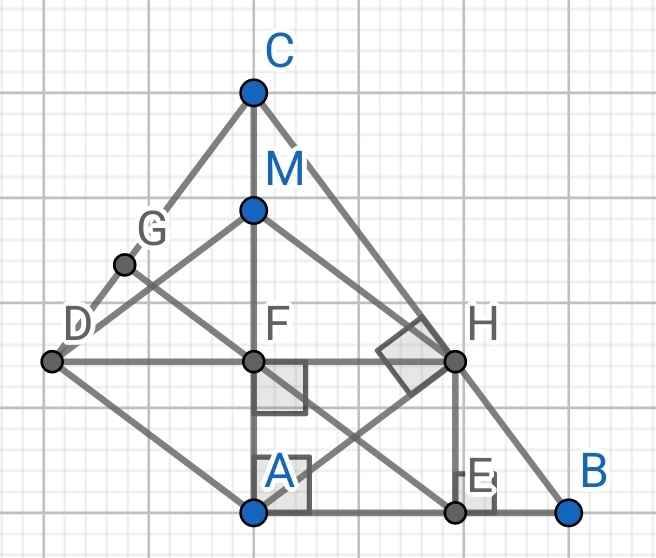a) Do HE ⊥ AB (gt)
⇒ ∠AEH = 90⁰
Do HF ⊥ AC (gt)
⇒ ∠AFH = 90⁰
Do ∆ABC vuông tại A (gt)
⇒ ∠EAF = 90⁰
Tứ giác AEHF có:
∠AEH = ∠AFH = ∠EAF = 90⁰
⇒ AEHF là hình chữ nhật
b) Do AEHF là hình chữ nhật (cmt)
⇒ HE = AF
Mà AF = FM (do A và M đối xứng qua F)
⇒ HE = FM
Do AEHF là hình chữ nhật (cmt)
⇒ HE // AF
⇒ HE // FM
Tứ giác EFMH có:
HE // FM (cmt)
HE = FM (cmt)
⇒ EFMH là hình bình hành
c) Do A và M đối xứng qua F (gt)
⇒ F là trung điểm của AM
Do D và H đối xứng qua F (gt)
⇒ F là trung điểm của DH
Do HF ⊥ AC (gt)
⇒ HD ⊥ AM
Tứ giác AHMD có:
F là trung điểm của AM (cmt)
F là trung điểm của DH (cmt)
⇒ AHMD là hình bình hành
Mà HD ⊥ AM (cmt)
⇒ AHMD là hình chữ thoi
⇒ AD // MH
Do EFMH là hình bình hành (cmt)
⇒ EF // MH
Mà AD // MH
⇒ EF // AD
Do ADMH là hình thoi (cmt)
⇒ AM là tia phân giác của ∠DAH
⇒ ∠DAM = ∠HAM
⇒ ∠DAC = ∠HAC
Do ADMH là hình thoi
⇒ AD = AH
Xét ∆ADC và ∆AHC có:
AD = AH (cmt)
∠DAC = ∠HAC (cmt)
AC là cạnh chung
⇒ ∆ADC = ∆AHC (c-g-c)
⇒ ∠ADC = ∠AHC = 90⁰ (hai góc tương ứng)
⇒ AD ⊥ DC
Mà EF // AD (cmt)
⇒ EF ⊥ DC