Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: ΔABC cân tại A
a: Sửa đề: AB là trung bình nhân của AE và AH
CF//BH
CF\(\perp\)AB
Do đó: BA\(\perp\)BH
=>ΔBAH vuông tại B
Xét ΔBAH vuông tại B có BE là đường cao
nên \(AE\cdot AH=AB^2\)
=>\(AB=\sqrt{AE\cdot AH}\)
=>AB là trung bình nhân của AE và AH
b: Từ C, kẻ CG\(\perp\)CB, \(G\in AB\)
ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
Xét ΔBCG có
D là trung điểm của BC
DA//CG
Do đó: A là trung điểm của BG
Xét ΔBCG có D,A lần lượt là trung điểm của BC,BG
=>DA là đường trung bình
=>CG=2DA
=>4DA^2=CG^2
Xét ΔCBG vuông tại C có CF là đường cao
nên \(\dfrac{1}{CF^2}=\dfrac{1}{CG^2}+\dfrac{1}{CB^2}\)
=>\(\dfrac{1}{CF^2}=\dfrac{1}{4DA^2}+\dfrac{1}{CB^2}\)

kẻ đường cao AH ta có \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
AD và AE là hai tia phân giác cả hai góc kề bù => AD _|_ AE
AH là đường cao của tam giác vuông ADE ta có
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AE^2}\)
vậy \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AD^2}+\frac{1}{AE^2}\)

Kẻ DM, DN vuông góc với AB, AC.
Ta có: DNAB=CDBD⇒1AB=CDDN.BC;MDAC=BDBC⇒1AC=BDMD.BC⇒1AB+1AC=CD+BDDN.BC=1DNDNAB=CDBD⇒1AB=CDDN.BC;MDAC=BDBC⇒1AC=BDMD.BC⇒1AB+1AC=CD+BDDN.BC=1DN
Do AMDN là hình vuông nên: AD=√2DMAD=2DM =>ĐPCM
Câu b thì cm tương tự, mình để bạn tự giải !

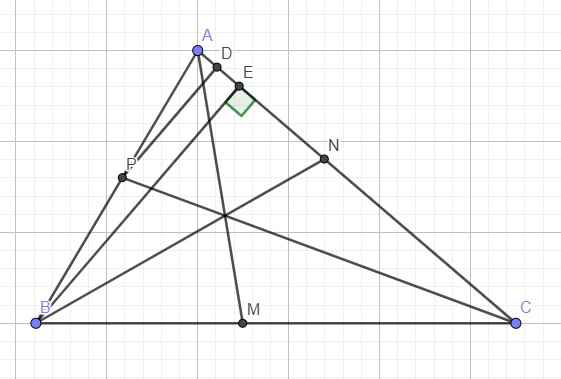
Kẻ PD và BE vuông góc AC
Định lý phân giác: \(\dfrac{AN}{NC}=\dfrac{AB}{BC}\Rightarrow\dfrac{AN}{AN+NC}=\dfrac{AB}{AB+BC}\Rightarrow\dfrac{AN}{AC}=\dfrac{AB}{AB+BC}=\dfrac{c}{a+c}\)
Tương tự: \(\dfrac{AP}{AB}=\dfrac{b}{a+b}\)
Talet: \(\dfrac{PD}{BE}=\dfrac{AP}{AB}\)
\(\dfrac{S_{APN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}PD.AN}{\dfrac{1}{2}BE.AC}=\dfrac{AP}{AB}.\dfrac{AN}{AC}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}\)
Tương tự: \(\dfrac{S_{BPM}}{S_{ABC}}=\dfrac{ac}{\left(a+b\right)\left(b+c\right)}\) ; \(\dfrac{S_{CMN}}{S_{ABC}}=\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{APN}+S_{BPM}+S_{CMN}}{S_{ABC}}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{S_{ABC}-\left(S_{APN}+S_{BPM}+S_{CMN}\right)}{S_{ABC}}=1-\left(\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\right)\)
\(=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
2. Do ABC cân tại C \(\Rightarrow AC=BC=a\)
\(\dfrac{BC}{AB}=k\Rightarrow AB=\dfrac{BC}{k}=\dfrac{a}{k}\)
Do đó:
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=\dfrac{2.a.a.\dfrac{a}{k}}{2a.\left(a+\dfrac{a}{k}\right)\left(a+\dfrac{a}{k}\right)}=\dfrac{k}{\left(k+1\right)^2}\)