Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác EMDN có
\(\widehat{EMD}=\widehat{END}=\widehat{MEN}=90^0\)
Do đó: EMDN là hình chữ nhật
mà ED là đường phân giác
nên EMDN là hình vuông

a: Xét tứ giác EMDN có
\(\widehat{EMD}=\widehat{END}=\widehat{MEN}=90^0\)
Do đó: EMDN là hình chữ nhật
mà ED là đường phân giác
nên EMDN là hình vuông

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

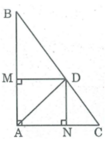
Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)
DM ⊥ AB (gt)
⇒ ∠ (AMD) = 90 0
DN ⊥ AC (gt) ⇒ ∠ (AND) = 90 0
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông

B D V N M K E C
a) Xét tứ giác ADME có :
Góc A = 900 ( tam giác ABC vuông tại A )
Góc D = 900 ( MD vuông góc AB )
Góc E = 900 ( ME vuông góc AC )
Do đó tứ giác ADME là hình chữ nhật
b) Chứng minh đúng D, E là trung điểm của AB ; AC
Chứng minh đúng DE là đường trung bình của tam giác
ABC nên DE song song và \(DE=\frac{BC}{2}\)
Cho nên DE song song với BM và DE = BM
=> Tứ giác BDME là hình bình hành
c) Xét tứ giác AMCF có :
E là trung điểm MF ( vì M đối xứng với F qua E )
Mà E là trung điểm của AC ( cmt )
Nên tứ giác AMCF là hình bình hành
Ta có AC vuông góc MF ( vì ME vuông góc AC )
Do đó tứ giác AMCF là hình thoi
d) Chứng minh đúng tứ giác ABNE là hình chữ nhật
Gọi O là giao điểm hai đường chéo AN và BE của hình chữ nhật ABNE
trong tam giác vuông BKE có KO là trung tuyến ứng với cạnh huyền BE
nên \(KO=\frac{BE}{2}\)
mà BE = AN ( đường chéo hình chữ nhật ) nên \(KO=\frac{AN}{2}\)
trong tam giác AKN có trung tuyến KO bằng nửa cạnh AN
nên tam giác AKN vuông tại A
Vậy AK vuông góc KN

bạn tự vẽ hình nk.
cm: vì m, n lần lượt là chân đg vuông góc kẻ từ d dến ab,ac
=> tứ giác AMDN là hình chữ nhật (có 3 góc vuông) (dh nb hcn)
mặt #: ad là đg phân giác của góc a
=> hcn AMDN là hình vuông vì có có đường chéo là đường phân giác của góc a(dh nb hv)

Xét tứ giác AMDN, ta có: ∠∠(MAN) = 900900 (gt)
DM ⊥ AB (gt)
⇒∠∠(AMD) = 900900
DN ⊥ AC (gt) ⇒∠∠(AND) = 900900
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
mk cần câu bạn ơi