Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

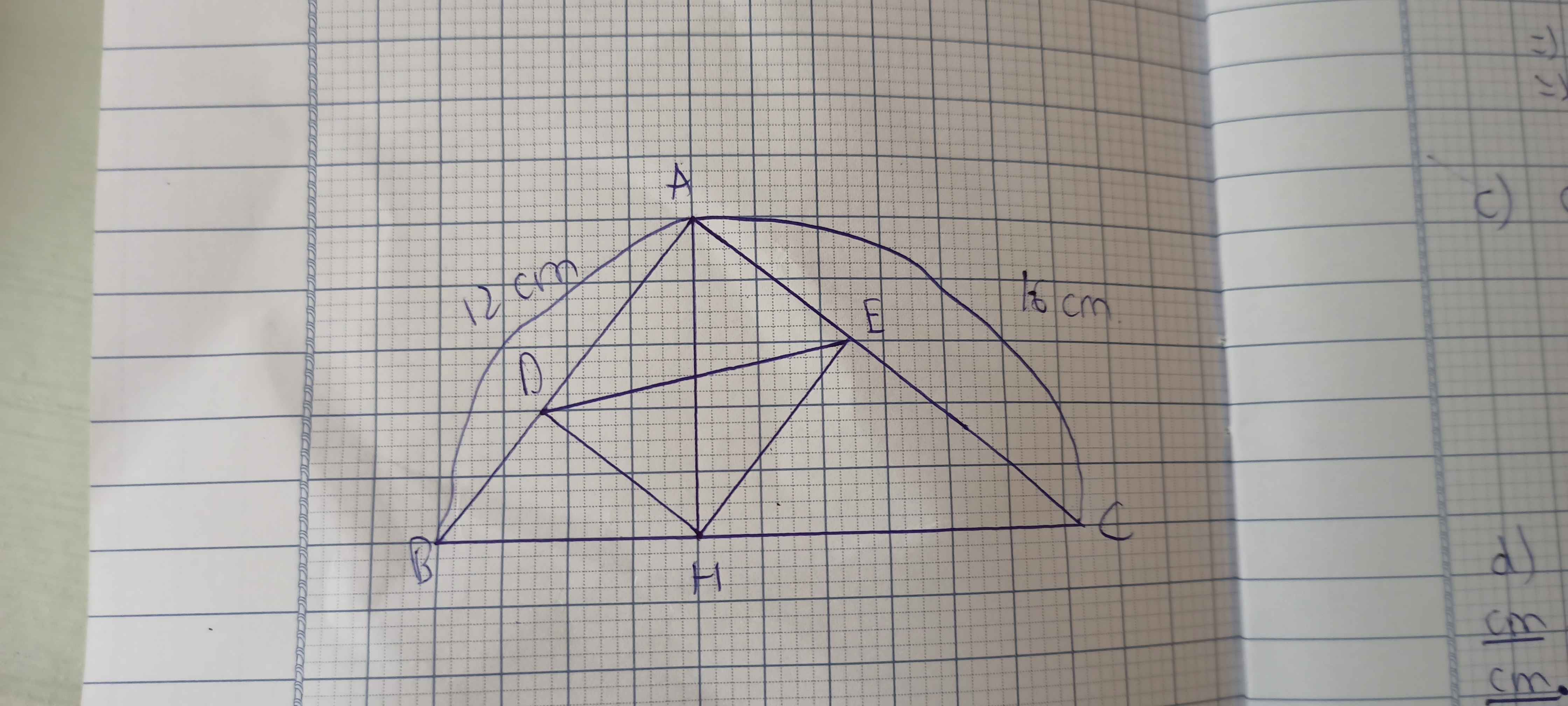
a)Xét tam giác HAC và tam giác ABC có :
Góc AHC = góc BAC ( = 90o)
Góc BCA chung
⇒ Tam giác HAC ~ Tam giác ABC ( TH3 )
b) Xét tam giác AHD và tam giác ABH có :
Góc HAB chung
Góc ADH = Góc AHB ( = 90o)
⇒ Tam giác AHD ~ Tam giác ABH ( TH3)
⇒ \(\dfrac{AH}{AB}=\dfrac{AD}{AH}\)
⇒ AH2 = AB.AD
c) Xét tam giác AEH và tam giác AHC có :
Góc HAC chung
Góc AEH = góc AHC ( = 90o)
⇒ Tam giác AEH ~ Tam giác AHC ( TH3)
⇒ \(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)
⇒ AH2 = AE.AC
Mà : AH2 = AD.AB ( Câu b)
⇒ AE.AC = AD.AB
d) Do : AE.AC = AD.AB ( Câu c)
⇒ \(\dfrac{AE}{AD}=\dfrac{AC}{AB}\)
Xét tam giác AED và tam giác ACB có :
Góc BAC chung
\(\dfrac{AE}{AD}=\dfrac{AC}{AB}\) ( cmt)
⇒Tam giác AED ~ Tam giác ACB ( TH2)
⇒ \(\dfrac{S_{AED}}{S_{ACB}}=\left(\dfrac{AE}{AC}\right)^2\)
P/S : Hình như thiếu dữ kiện , chưa cho AH nên ko ra số cụ thể
â)xét tam giác hac và tam giác abc có:
góc c chung
góc ahc= góc bac=90 độ
suy ra tam giác hac đồng dạng với tam giác abc(g.g)
b)xét tam giác ahb và tam giác adh có
góc ahb= góc adh=90 độ
góc a chung
suy ra tam giác ahb đồng dạng với tam giác adh(g.g)
ta có:ah^2=ab.ad


a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
![]()
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
![]()



a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
Do đó: ΔHAC\(\sim\)ΔABC
b: Xét ΔABH vuông tại H có HD là đường cao
nên \(AH^2=AD\cdot AB\left(1\right)\)
c: Xét ΔACH vuông tại H có HE là đườg cao
nên \(AH^2=AE\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
bạn ơi sao vuông tại h có đường cao lại suy ra đc ah bình =ad.ab rứa mik khoog hiểu =((

a) Xét ΔAHB vuông tại H và ΔADH vuông tại D có
\(\widehat{DAH}\) chung
Do đó: ΔAHB\(\sim\)ΔADH(g-g)

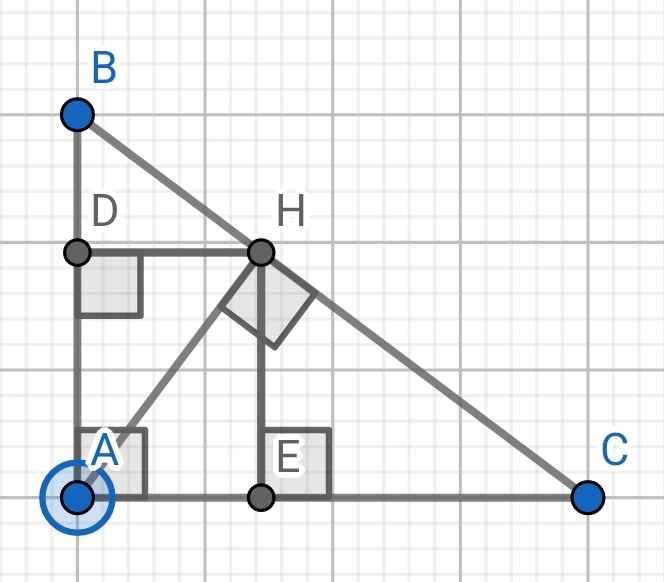
a) Xét hai tam giác vuông: ∆HAC và ∆ABC có:
∠C chung
∆HAC ∽ ∆ABC (g-g)
b) Xét hai tam giác vuông: ∆AHB và ∆ADH có:
∠A chung
⇒ ∆AHB ∽ ∆ADH (g-g)
⇒ AH/AD = AB/AH
⇒ AH.AH = AD.AB
Hay AH² = AD.AB (1)
c) Xét hai tam giác vuông: ∆AHC và ∆AEH có:
∠A chung
⇒ ∆AHC ∽ ∆AEH (g-g)
⇒ AH/AE = AC/AH
⇒ AH.AH = AE.AC
Hay AH² = AE.AC (2)
Từ (1) và (2) ⇒ AD.AB = AE.AC
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng với ΔABC
b: ΔAHB vuông tại H
mà HD là đường cao
nên AH^2=AD*AB
c: ΔACH vuông tại H có HE là đường cao
nên AE*AC=AH^2=AD*AB

a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat{HAB}=\widehat{BAC}=90^0\)
\(\widehat{B}:chung\)
do đó \(\Delta HBA\sim\Delta ABC\left(g-g\right)\)
b) Xét \(\text{ΔHBAvàΔHAC}\) có:
\(\widehat{BHA}=\widehat{CHA}=90^o\)
\(\widehat{ABH}=\widehat{HAC}\) ( do cùng phụ với \(\widehat{BAH}\))
Do đó: \(\Delta HBA\sim\Delta HAC\left(g-g\right)\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB\cdot HC\)
c) Xét tứ giác ADHE có:
\(\widehat{A}=\widehat{D}=\widehat{E}=90^o\)
Do đó ADHE là hình chữ nhật
Gọi O là giao điểm 2 đường chéo hình chữ nhật(AH và DE)
\(\Rightarrow OD=OA\)(tính chất HCN)
\(\Rightarrow\Delta ODA\) cân tại O
\(\Rightarrow\widehat{ODA}=\widehat{OAD}\)
Xét \(\Delta ADE\) và \(\Delta HAB\) có:
\(\widehat{BHA}=\widehat{DAE}=90^o\\ \widehat{ODA}=\widehat{OAD}\left(cmt\right)\\ \Rightarrow\Delta ADE\sim\Delta HAB\)
Mà \(\Delta HBA\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\) (tính chất bắc cầu)

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4.8\left(cm\right)\\BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b:
Áp dụng hệ thức lượng trong tam giác vuông ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông ΔABH vuông tại A có HD là đường cao ứng với cạnh huyền BA, ta được:
\(AD\cdot AB=AH^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AE\cdot AC=AD\cdot AB\)
hay \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Xét ΔAED vuông tại A và ΔABC vuông tại A có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: ΔAED\(\sim\)ΔABC