Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

g) Nhớ lại rằng hai tam giác đồng dạng thì tỉ số diện tích bằng bình phương tỉ số đồng dạng.
Ta có \(\Delta IAB\sim\Delta BAC\to\frac{S\left(IAB\right)}{S\left(ABC\right)}=\left(\frac{AB}{AC}\right)^2.\)
Tương tự \(\Delta BAC\sim\Delta BHA\to\frac{S\left(ABC\right)}{S\left(HBA\right)}=\left(\frac{BC}{BA}\right)^2.\)
Nhân hai đẳng thức với nhau cho ta \(\frac{S\left(IAB\right)}{S\left(ABH\right)}=\left(\frac{BC}{AC}\right)^2=\frac{BC^2}{AC^2}=\frac{BC^2}{BC\cdot CH}=\frac{BC}{CH}\to\frac{S\left(ABH\right)}{S\left(IAB\right)}=\frac{CH}{BC}.\) (ĐỀ SAI NHÉ)
h) Theo định lý Pi-ta-go ta có
\(BC^2=\left(BH+CH\right)^2=BH^2+CH^2+2BH\cdot CH=BE^2+EH^2+HF^2+FC^2+2AH^2\)
\(=BE^2+CF^2+2AH^2+\left(HE^2+HF^2\right)=BE^2+CF^2+2AH^2+EF^2=BE^2+CF^2+3AH^2.\)

b: Xét ΔBAC vuông tại B có BH là đường cao
nên \(HA\cdot HC=BH^2\left(1\right)\)
Xét ΔBHC vuông tại H có HE là đường cao
nên \(BE\cdot BC=BH^2\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HC=BE\cdot BC\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)

Bài 3:
Ta có:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\)
\(\Rightarrow\widehat{P}=180^o-90^o-37^o=53^o\)
Mà: \(sinN=\dfrac{MN}{NP}\)
\(\Rightarrow sin37^o=\dfrac{MN}{25}\)
\(\Rightarrow MN=25\cdot sin37^o\approx15\left(cm\right)\)
Áp dung định lý Py-ta-go ta có:
\(MP=\sqrt{NP^2-MN^2}=\sqrt{25^2-15^2}=20\left(cm\right)\)
3:
a: Xét ΔABC có AC^2=BA^2+BC^2
nên ΔBAC vuông tại B
b: Xét ΔBAC vuông tại B có
sin A=BC/AC=42/58=21/29
cos A=AB/AC=40/58=20/29
tan A=BC/BA=21/20
cot A=BA/BC=20/21
c: Xét ΔABC vuông tại B có BH là đường cao
nên BH*AC=BA*BC; BA^2=AH*AC; CB^2=CH*CA
=>BH*58=40*42=1680
=>BH=840/29(cm)
BA^2=AH*AC
=>AH=BA^2/AC=40^2/58=800/29cm
CB^2=CH*CA
=>CH=CB^2/CA=42^2/58=882/29(cm)
ΔBHA vuông tại H có HE là đường cao
nênBE*BA=BH^2
=>BE*40=(840/29)^2
=>BE=17640/841(cm)
ΔBHC vuông tại H có HF là đường cao
nênBF*BC=BH^2
=>BF*42=(840/29)^2
=>BF=16800/841(cm)
Xét tứ giác BEHF có
góc BEH=góc BFH=góc EBF=90 độ
=>BEHF là hình chữ nhật
=>góc BFE=góc BHE(=1/2*sđ cung BE)
=>góc BFE=góc BAC
Xét ΔBFE và ΔBAC có
góc BFE=góc BAC
góc FBE chung
Do đó: ΔBFE đồng dạng với ΔBAC
=>S BFE/S BAC=(BF/BA)^2=(16800/441:40)^2=(420/841)^2
=>S AECF=S ABC*(1-(420/841)^2)
=>\(S_{AECF}=\dfrac{1}{2}\cdot40\cdot42\cdot\left[1-\left(\dfrac{420}{841}\right)^2\right]\simeq630,5\left(cm^2\right)\)

hình tự vẽ nhé:
\(BC=BH+HC=16+81=97\)
Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(AB^2=16.97=1552\)
\(\Rightarrow\)\(AB=\sqrt{1552}=4\sqrt{97}\)
\(AC^2=HC.BC\)
\(\Rightarrow\)\(AC^2=81.97=7857\)
\(\Rightarrow\)\(AC=\sqrt{7857}=9\sqrt{97}\)
\(AH.BC=AB.AC\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}\)
\(\Rightarrow\)\(AH=\frac{4\sqrt{97}.9\sqrt{97}}{97}=36\)
\(AD.AB=AH^2\)
\(AE.AC=AH^2\)
suy ra: \(AD.AB=AE.AC\)
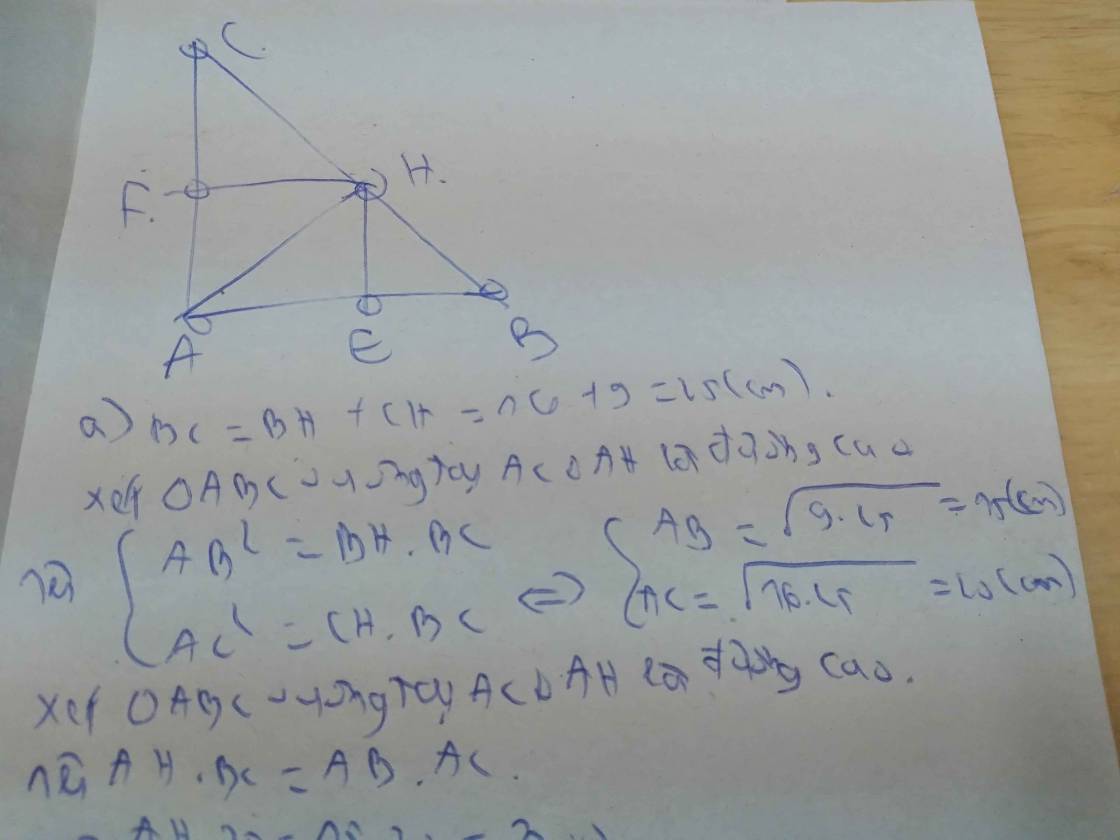



a) Tam giác ABH vuông tại H, HE là đường cao
\(\Rightarrow AH^2=AE.AB\)(1)
Tam giác AHC vuông tại H, HF là đường cao
\(\Rightarrow AH^2=AF.AC\)(2)
từ (1) và (2) nên AE.AB=AF.AC(đpcm)
b) Tam giác ABC vuông tại A, AH là đường cao
\(\Rightarrow AB^2=BH.BC\)(3)
Tam giác BIC vuông tại B, BA là đường cao
\(\Rightarrow AB^2=IA.IC\) mà theo (3) thì \(BH.BC=IA.IC\left(\text{đ}pcm\right)\)
c) Tam giác ABC vuông tại A, đường cao AH
\(AH^2=BH.CH\Leftrightarrow AH^2=9.16=144\Leftrightarrow AH=12\)(cm)
BC=9+16=25(cm)
Tam giác ABC vuông tại A, AH là đường cao
\(AB^2=BH.BC=9.25=225\Leftrightarrow AB=15\)
\(AC^2=CH.BC=16.25=400\Leftrightarrow AC=20\)
Tam giác ABC có AD là phân giác
\(\frac{AB}{AC}=\frac{BD}{CD}\Leftrightarrow\frac{15}{20}=\frac{BD}{CD}\Leftrightarrow\frac{15}{BD}=\frac{20}{CD}=\frac{15+20}{BD+CD}=\frac{35}{25}=\frac{7}{5}\)
\(\Leftrightarrow BD=\frac{15.5}{7}=\frac{75}{7}\)\(\Leftrightarrow DH=BD-BH=\frac{75}{7}-9=\frac{12}{7}\)
Áp dụng định lý Py-ta-go vào tam giác vuông AHD:
\(AD^2=DH^2+AH^2=\frac{144}{49}+144=\frac{7200}{49}\Rightarrow AD=\frac{60\sqrt{2}}{7}\)
d) Tam giác ABC vuông tại A, AH là đường cao
\(AB^2=BH.BC\);\(AC^2=CH.BC\)
\(\Rightarrow\frac{AB^2}{AC^2}=\frac{HB.BC}{CH.BC}=\frac{BH}{CH}\left(\text{đ}pcm\right)\)
Còn câu e chờ mình xíu
c) Ta sẽ chứng minh bổ đề sau để dễ dàng tính: Cho \(\Delta\)ABC vuông tại A đường phân giác AD. Chứng minh: \(\frac{1}{AB}+\frac{1}{AC}=\frac{\sqrt{2}}{AD}\)
C/m: Tự kẻ hình nha .Kẻ DH // AB => DH vuông góc AC. Vì \(\Delta\)ADH vuông tại H có góc DAH=90 nên \(\Delta\)ADH vuông cân tại H
=> \(AD=\sqrt{2}DH\Rightarrow DH=\left(\frac{AD}{\sqrt{2}}\right)\)
Ta có DH // AB => \(\frac{DH}{AB}=\frac{HC}{AC}=\frac{AC-AH}{AC}\) vì (HC=AC-AH)