Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: ADHE là hình chữ nhật
nen AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
=>ΔABC cân tại A
=>AB=AC

1a) A=D=E=90 độ
=>AEHD là hcn
=>AH=DE
b)Xét tam giác DBH vuông tại D có:
DI là đường trung tuyến ứng với cạnh huyền BH
=>DI=BH/2=IH
=>tam giác IDH cân tại I
=>góc IDH=góc IHD (1)
Gọi O là gđ 2 đường chéo AH và DE
=>OD=OA=OE=OH (tự c/m)
=> tam giác DOH cân tại O
=> góc ODH=góc OHD(2)
từ (1) và (2) => góc ODH+góc IDH=90 độ(EHD+DHI=90 độ)
=>IDvuông góc DE(3)
Cmtt ta được: KEvuông góc DE(4)
Từ (3)và (4) => DI//KE.
2a) Ta có góc HAB+góc HAC=90 độ (1)
Xét tam giác ABC vuông tại A có
AM là đg trung tuyến ứng vs cạnh huyền BC
=>AM=MC
=>tam giác AMC cân
=>góc MAC=góc ACM
Lại có: góc HAC+góc ACH=90 độ(2)
Từ (1) và (2) => góc BAH=góc ACM
Mà góc AMC=góc MAC(cmt)
=>ABH=MAC(3)
b)A=D=E=90 độ
=>AFHE là hcn
Gọi O là gđ EF và AM
OA=OF(tự cm đi nha)
=>tam giác OAF cân
=>OAF=OFA(4)
Ta có : OAF+MCA=90 độ(5)
Từ (3)(4) và (5)
=>MAC+OFA=90 độ
Hay AM vuông góc EF
k giùm mình nha.

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
=>AH cắt DE tại trung điểm của mỗi đường và AH=DE
=>OA=OE
b: AD*AB=AH^2
AE*AC=AH^2
Do đó: AD*AB=AE*AC
=>AD/AC=AE/AB
=>ΔADE đồng dạng với ΔACB

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
b: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành

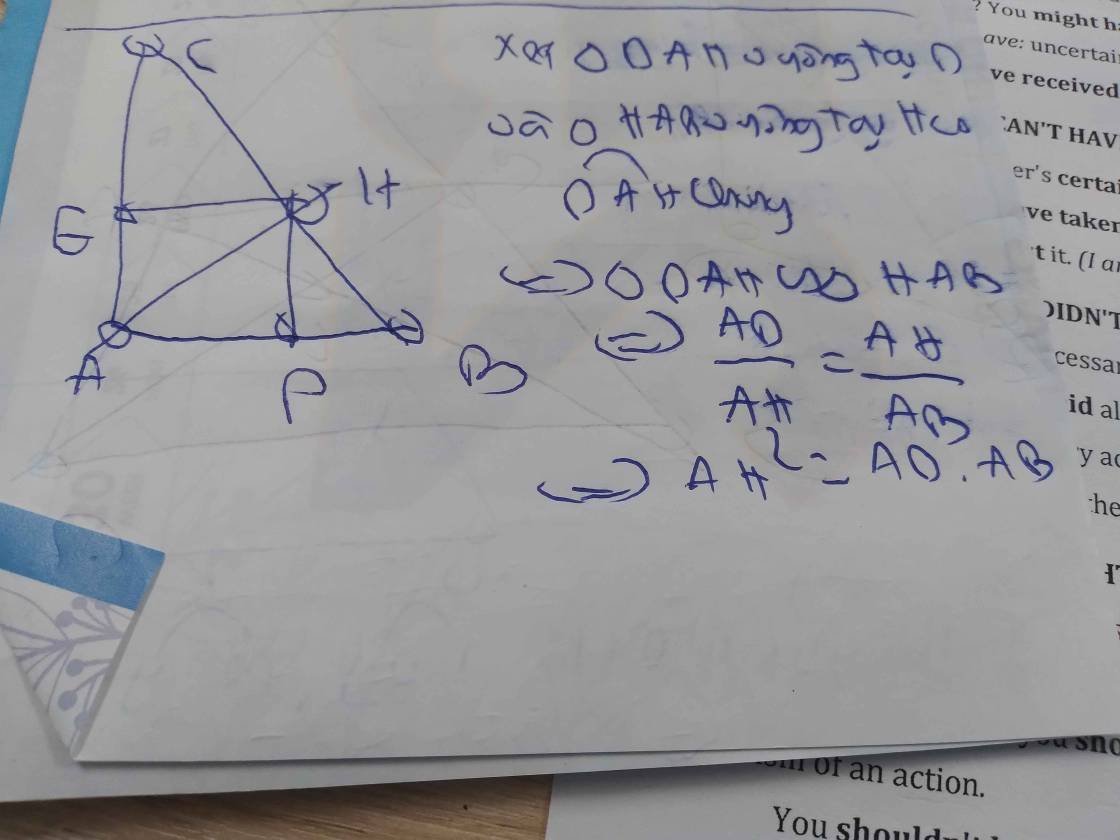
mọi người giúp em dùm cái ạ -_-
\(\widehat{DAH}=90^0-\widehat{AHD}=\widehat{BHD}\).
\(\widehat{HAE}=90^0-\widehat{AHE}=\widehat{CHE}\).
-△AHD và △HBD có: \(\widehat{DAH}=\widehat{DHB};\widehat{ADH}=\widehat{BDH}=90^0\).
\(\Rightarrow\)△AHD∼△HBD (g-g) \(\Rightarrow\dfrac{AD}{HD}=\dfrac{HD}{BD}\Rightarrow HD^2=AD.BD\).
-△AHE và △HCE có: \(\widehat{HAE}=\widehat{CHE};\widehat{AEH}=\widehat{HEC}=90^0\).
\(\Rightarrow\)△AHE∼△HCE (g-g) \(\Rightarrow\dfrac{AE}{HE}=\dfrac{HE}{CE}\Rightarrow HE^2=AE.CE\)
\(\Rightarrow HD^2+HE^2=AD.BD+AE.CE\left(1\right)\).
-Tứ giác ADHE có: \(\widehat{ADH}=\widehat{DAE}=\widehat{AEH}=90^0\)
\(\Rightarrow\)ADHE là hình chữ nhật nên △DHE vuông tại H, \(AH=DE\)
\(\Rightarrow HD^2+HE^2=DE^2=AH^2\left(2\right)\)
-Từ (1), (2) suy ra: \(AH^2=AD.BD+AE.CE\)