Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

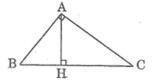
Tam giác ABH và CAH vuông và có ^BAH=^C (cùng phụ với góc B)
Nên Tam giác ABH và CAH đồng dạng (g-g) =>AB/AC = k (tỷ số đồng dạng)
Mà C(ABH) / C(CAH) = k (tỷ số chu vi bằng tỷ số đồng dạng)
suy ra 30/40 = k hay k = 3/4.
do đó AB/AC = 3/4 hay AB/3 = AC/4 = t
=> AB = 3t; AC = 4t Theo Pitago ta tính được BC = 5t.
Vậy chu vi tam giác ABC là AB+AC+BC = 3t+4t+5t = 12t.

Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:


\(BC=\dfrac{15^2}{9}=25\left(cm\right)\)
BH=25-9=16cm
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
AB=căn(16^2+12^2)=20cm
C=16+12+20=28+20=48cm
Xét ΔABC vuông tại A có sin B=AC/BC=3/5
nên góc B=37 độ

cách 1
Đề bài có đủ điều kiện để tính. Sau khi xác định được tỷ lệ các cạnh tg ABC là a:b:c=5:4:3, đặt AB=3t, AC=4t; BC=5t (như bạn Hải đã chứng minh). Vì tam giác ABC vuông ta có AB^2=BH.BC ---> (3t)^2=BH.(5t) ---> BH=1,8.t
----> AH^2=AB^2-BH^2 =(3t)^2 -(1,8t)^2 = 9t^2 -3,24t^2 =5,76t^2 --> AH= 2,4t
Chu vi ABH=30 --> AB+BH+AH=30 --> 3t+1,8t+2,4t=30 --->7,2t=30 ---> t= 25/6
Chu vi ABC= 3t+4t+5t= 12t =12.(25/6) =50 cm
cách 2
Tam giác ABH và CAH vuông và có ^BAH=^C (cùng phụ với góc B)
Nên Tam giác ABH và CAH đồng dạng (g-g) =>AB/AC = k (tỷ số đồng dạng)
Mà C(ABH) / C(CAH) = k (tỷ số chu vi bằng tỷ số đồng dạng)
suy ra 30/40 = k hay k = 3/4.
do đó AB/AC = 3/4 hay AB/3 = AC/4 = t
=> AB = 3t; AC = 4t Theo Pitago ta tính được BC = 5t.
Vậy chu vi tam giác ABC là AB+AC+BC = 3t+4t+5t = 12t.
k mk nha!!^-^
Sau khi xác định được tỷ lệ các cạnh tg ABC là a:b:c=5:4:3, đặt AB=3t, AC=4t; BC=5t . Vì tam giác ABC vuông ta có AB^2=BH.BC => (3t)^2=BH.(5t) => BH=1,8.t
=> AH^2=AB^2-BH^2 =(3t)^2 -(1,8t)^2 = 9t^2 -3,24t^2 =5,76t^2 --> AH= 2,4t
Chu vi ABH=30 --> AB+BH+AH=30 --> 3t+1,8t+2,4t=30 --->7,2t=30 ---> t= 25/6
Chu vi ABC= 3t+4t+5t= 12t =12.(25/6) =50 cm
Đáp số : 50 cm

\(\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{4}{3}\)
\(\Leftrightarrow\dfrac{BD}{CD}=\dfrac{4}{3}\)
hay BD=100(cm)
Suy ra: HD=BD-BH=112-100=12(cm)
\(AD=\sqrt{AH^2+HD^2}=\sqrt{84^2+12^2}=60\sqrt{2}\left(cm\right)\)