Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

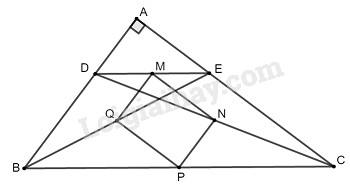
Xét ΔCDB có CN/CD=CP/CB
nên NP//BD và NP=DB/2
Xét ΔEDB có EM/ED=EQ/EB
nên MQ//BD và MQ=BD/2
=>NP//MQ và NP=MQ
Xét ΔDEC có DN/DC=DM/DE
nên MN//EC
=>MN vuông góc với AB
=>MN vuông góc với NP
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
MN vuông góc với NP
Do đó: MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc 1 đường tròn

Xét ΔCDB có CN/CD=CP/CB
nên NP//BD và NP=DB/2
Xét ΔEDB có EM/ED=EQ/EB
nên MQ//BD và MQ=BD/2
=>NP//MQ và NP=MQ
Xét ΔDEC có DN/DC=DM/DE
nên MN//EC
=>MN vuông góc với AB
=>MN vuông góc với NP
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
MN vuông góc với NP
Do đó: MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc 1 đường tròn

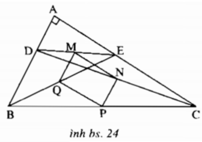
* Xét tam giác DECDEC có
MM là trung điểm DEDE
NN là trung điểm DCDC
Suy ra, MNMN là đường trung bình của tam giác DECDEC, hay MN//ECMN//EC (*) và MN=12ECMN=12EC (1)
* Xét tam giác BECBEC có
QQ là trung điểm BEBE
PP là trung điểm BCBC
Suy ra, PQPQ là đường trung bình của tam giác BECBEC, hay PQ//ECPQ//EC và PQ=12ECPQ=12EC (2).
Từ (1) và (2) suy ra tứ giác MNPQMNPQ là hình bình hành.
* Xét tam giác DEBDEB có
QQ là trung điểm BEBE
MM là trung điểm DEDE
Suy ra, QMQM là đường trung bình của tam giác BEDBED, hay MQ//DBMQ//DB (3).
Mà AB⊥ACAB⊥AC (4)
Từ (*), (3) và (4) suy ra MN⊥MQMN⊥MQ (5)
Tứ giác MNPQMNPQ là hình bình hành mà có một góc vuông suy ra MNPQMNPQ là hình chữ nhật.
Gọi II là giao điểm của hai đường chéo MPMP và QN,QN, các điểm M,N,P,QM,N,P,Q đều cách đều II một khoảng cố định, suy ra M,N,P,QM,N,P,Q cùng thuộc một đường tròn
Xem thêm tại: https://loigiaihay.com/giai-bai-12-phan-bai-tap-bo-sung-trang-158-sbt-toan-9-tap-1-a72611.html#ixzz65S8F62Pu

Xét ΔCDB có CN/CD=CP/CB
nên NP//BD và NP=BD/2
Xét ΔEDB có EM/ED=EQ/EB
nên MQ//BD và MQ=1/2BD
=>NP//MQ và NP=MQ
Xét ΔDEC có DM/DE=DN/DC
nên MN//EC
=>MN vuông góc với NP
Xét tứ giác MNPQ có
PN//MQ
PN=MQ
góc MNP=90 độ
Do đó: MNPQ là hình chữ nhật
=>MNPQ là tứ giác nội tiếp

Xét ΔCDB có
N là trung điểm của CD
P là trung điểm của CB
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(1)
Xét ΔEDB có
M là trung điểm của ED
Q là trung điểm của EB
DO đó: MQ là đường trung bình
=>MQ//DB và MQ=DB/2(2)
Từ (1) và (2) suy ra NP//MQ và NP=MQ
Xét ΔCEB có
P là trung điểm của BC
Q là trung điểm của BE
Do đó PQ là đường trung bình
=>PQ//AC
=>PQ\(\perp\)AB
=>PQ\(\perp\)PN
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
DO đó: MNPQ là hình bình hành
mà \(\widehat{NPQ}=90^0\)
nên MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc một đường tròn

Xét ΔCDB có
N là trung điểm của CD
P là trung điểm của CB
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(1)
Xét ΔEDB có
M là trung điểm của ED
Q là trung điểm của EB
DO đó: MQ là đường trung bình
=>MQ//DB và MQ=DB/2(2)
Từ (1) và (2) suy ra NP//MQ và NP=MQ
Xét ΔCEB có
P là trung điểm của BC
Q là trung điểm của BE
Do đó PQ là đường trung bình
=>PQ//AC
=>PQ\(\perp\)AB
=>PQ\(\perp\)PN
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
DO đó: MNPQ là hình bình hành
mà \(\widehat{NPQ}=90^0\)
nên MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc một đường tròn

Gọi N là điểm đối xứng với C qua F. Ta có EF = NE + NF = BC/2 = BE + CF = BE + NF, suy ra B và N đối xứng qua E
Lại có \(CP.CA=CF.CB=\frac{CN}{2}.2CM=CM.CN\). Do vậy 4 điểm A,P,M,N đồng viên
Hoàn toàn tương tự A,Q,M,N đồng viên. Từ đó 5 điểm A,M,N,P,Q đồng viên hay 4 điểm A,M,P,Q đồng viên (đpcm).
Tham khảo:
Xét tam giác DEC có
M là trung điểm DE
N là trung điểm DC
* Xét tam giác BEC có
Q là trung điểm BE
P là trung điểm BC
Từ (1) và (2) suy ra tứ giác MNPQ là hình bình hành.
* Xét tam giác DEB có
Q là trung điểm BE
M là trung điểm DE
Mà AB⊥AC (4)
Từ (1), (3) và (4) suy ra MN⊥MQ (5)
Tứ giác MNPQ là hình bình hành mà có một góc vuôngformat('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math114319d9cfc6123106878dc20b9%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2210.5%22%20y%3D%2216%22%3E%26%23x21D2%3B%3C%2Ftext%3E%3C%2Fsvg%3E) MNPQ là hình chữ nhật.
MNPQ là hình chữ nhật.
Gọi I là giao điểm của hai đường chéo MP và QN
Suy ra IM=IN=IP=IQ (tính chất hình chữ nhật)
Nên các điểm M, N, P, Q đều cách đều I một khoảng cố định