Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{C}+35^0=90^0\)
hay \(\widehat{C}=55^0\)
Vậy: \(\widehat{C}=55^0\)
b) Xét ΔBEA và ΔBED có
BA=BD(gt)
\(\widehat{ABE}=\widehat{DBE}\)(BE là tia phân giác của \(\widehat{ABD}\))
BE chung
Do đó: ΔBEA=ΔBED(c-g-c)
c) Xét ΔBHF vuông tại H và ΔBHC vuông tại H có
BH chung
\(\widehat{FBH}=\widehat{CBH}\)(BH là tia phân giác của \(\widehat{FBC}\))
Do đó: ΔBHF=ΔBHC(Cạnh góc vuông-góc nhọn kề)

a: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
b: Xét ΔBFC có
BH là đường cao
BH là đường phân giác
Do đó: ΔBFC cân tại B
c: Ta có: ΔBFC cân tại B
=>BF=BC
Xét ΔBDF và ΔBAC có
BD=BA
\(\widehat{DBF}\) chung
BF=BC
Do đó: ΔBDF=ΔBAC
=>\(\widehat{BDF}=\widehat{BAC}=90^0\)
Ta có: ΔBAE=ΔBDE
=>\(\widehat{BAE}=\widehat{BDE}\)
mà \(\widehat{BAE}=90^0\)
nên \(\widehat{BDE}=90^0\)
mà \(\widehat{BDF}=90^0\)
và DE,DF có điểm chung là D
nên D,E,F thẳng hàng

a: Xét ΔBEA và ΔBED có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBEA=ΔBED

https://olm.vn/hoi-dap/tim-kiem?id=205295114093&id_subject=1&q=++++++++++Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+t%E1%BA%A1i+A.Tia+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+ABC+c%E1%BA%AFt+AC+t%E1%BA%A1i+D.Tr%C3%AAn+c%E1%BA%A1nh+BC+l%E1%BA%A5y+%C4%91i%E1%BB%83m+E+sao+cho+BE=BAa)cmr+tam+gi%C3%A1c+ABD=EBDb)+Qua+%C4%91i%E1%BB%83m+C+k%E1%BA%BB+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+BD+t%E1%BA%A1i+H,+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+BD+c%E1%BA%AFt+tia+BA+t%E1%BA%A1i+F+cmr+BC=BEc)cmr+tam+gi%C3%A1c+ABC=EBFd)cmr+D,E,F+th%E1%BA%B3ng+h%C3%A0ng+%F0%9F%98%82+++++++++ BN THAM KHẢO Ở LINK NÀY

Xét ΔDBE và ΔABE có
BA=BD(gt)
\(\widehat{ABE}=\widehat{DBE}\)(BE là tia phân giác của \(\widehat{ABD}\))
BE chung
Do đó: ΔDBE=ΔABE(c-g-c)
⇒\(\widehat{BDE}=\widehat{BAE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BDE}=90^0\)
hay ED⊥BC tại D
Xét ΔCFB có
BH là đường cao ứng với cạnh CF(CH⊥BE, F∈CH, H∈BE)
CA là đường cao ứng với cạnh FB(CA⊥AB, F∈AB)
BH cắt CA tại E
Do đó: E là trực tâm của ΔCFB(Tính chất ba đường cao của tam giác)
⇒FE⊥BC
mà ED⊥BC
và FE,ED có điểm chung là E
nên D,E,F thẳng hàng(đpcm)
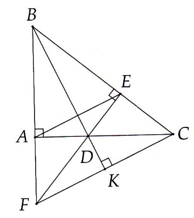

a . Xét ΔABC ⊥ tại A , ta có :
\(\widehat{ABC} \) + \(\widehat{ACB}\) = 90o ( 2 góc nhọn phụ nhau )
35o + \(\widehat{ACB}\) = 90o
⇒ \(\widehat{ACB}\) = 55o
b . Xét ΔBEA và ΔBED, ta có :
\(\left\{{}\begin{matrix}BA=BD\left(gt\right)\\\widehat{ABE}=\widehat{DBE}\\BE-BE\end{matrix}\right.\)
⇒ ΔBEA = ΔBED ( cạnh chung )
thêm vào chỗ góc ABE = góc DBE là ( BE là tia pg của góc ABC ) và BE=BE ( cạnh chung ) hộ mình nhá :3