Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tam giác ABC vuông tại A
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow BC^2-AC^2=AB^{^{ }2}\)
\(\Rightarrow13^2-5^2=BC^2\)
\(\Rightarrow BC^2=144\)
Vậy BC=12

a. áp dụng định lí pytago vào △ABC vuông tại A
\(BC^2=AB^2+AC^2\)
\(AB^2=BC^2-AC^2\)
\(AB^2=10^2-5^2=75\)
\(AB=\sqrt{75}\)(cm)
b. ta có : OA=OB=OC (gt)
➝điểm O cách đều 3 đỉnh của △ABC
➝O là giao điểm của 3 đường trung trực của △ ABC

a)
Trong tam giác ABC cân tại A có AD là đường trung tuyến.
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân);
AD chung;
BD = DC (D là trung điểm của BC).
Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\).
Vậy AD là đường cao của tam giác và đường phân giác của góc A.
Suy ra: AD là đường trung trực của tam giác ABC.
Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC.
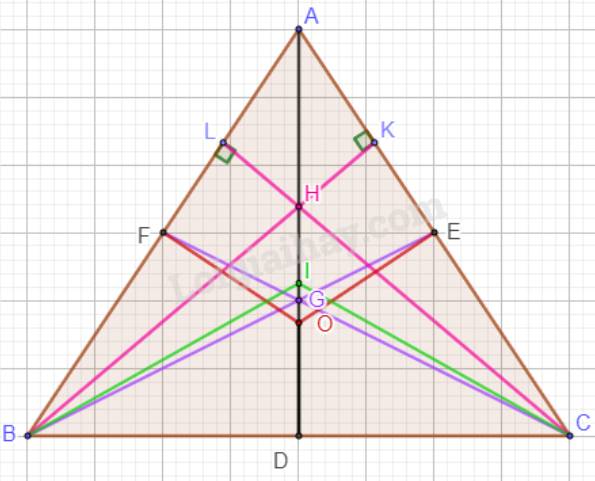
Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng.
Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
b)
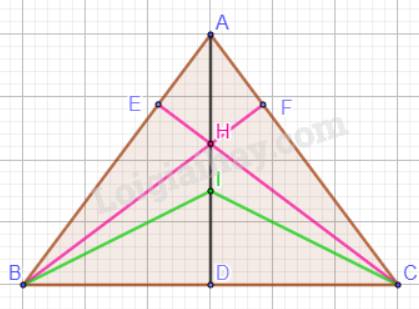
Ta có: \(AD \bot BC\).
H là trực tâm của tam giác ABC nên A, H, D thẳng hàng.
Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng.
Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC).
Nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác BAD và tam giác CAD có:
\(\widehat {BAD} = \widehat {CAD}\);
AD chung;
\(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)).
\(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng).
Do đó, tam giác ABC cân tại A
Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
a) Tam giác ABC vuông tại A => AB2=BC2-AC2 => AB2=132-52 <=> AB2=169-25=144 => AC=12
b) Giao điểm của 3 đường trung trực trong tam giác cách đều 3 đỉnh của tam giác đó. Mà OA=OB=OC
=> O là giao điểm của 3 đường trung trực trong tam gaics ABC.
c) Tam giác ABC vuông tại A => Giao của 3 đường trung trực trong tam giác ABC nằm trên cạnh BC
Mà OB=OC => Trung điểm của BC trùng với điểm O => AO là trung tuyến của tam giác ABC.
G là trọng tâm => GO=1/3AO=1/3BO=1/3CO. BO=CO=1/2BC =>BO=CO=13/2=6,5 (cm)
=> GO=1/3.6,5\(\approx\)2,1 (cm)
khó quá đi à