Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

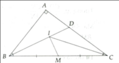
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{6}=\dfrac{DC}{10}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=8cm(D nằm giữa A và C)
nên \(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{8}{8}=1\)
=>\(DA=3\cdot1=3cm;DC=5\cdot1=5cm\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}=5\left(cm\right)\)
mà DC=5cm
nên CM=CD
Xét ΔCDI và ΔCMI có
CD=CM
\(\widehat{DCI}=\widehat{MCI}\)
CI chung
Do đó: ΔCDI=ΔCMI
=>\(\widehat{CID}=\widehat{CIM}\) và \(\widehat{IMC}=\widehat{IDC}\)(3)
Ta có: \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}\)(góc IDC là góc ngoài tại đỉnh D của ΔABD)
nên \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}=90^0+\widehat{ABD}\)(2)
Xét ΔBIM có \(\widehat{IMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{IMC}=\widehat{MIB}+\widehat{MBI}\left(1\right)\)
Từ (1),(2),(3) suy ra \(\widehat{MIB}+\widehat{MBI}=90^0+\widehat{ABD}\)
mà \(\widehat{MBI}=\widehat{ABD}\)
nên \(\widehat{MIB}=90^0\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10cm
Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{DA}{6}=\dfrac{DC}{10}\)
Ta có: D nằm giữa A và C(gt)
nên DA+DC=AC
hay DA+DC=8(cm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DA}{6}=\dfrac{DC}{10}=\dfrac{DA+DC}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{DA}{6}=\dfrac{1}{2}\\\dfrac{DC}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DA=6\cdot\dfrac{1}{2}=3\left(cm\right)\\DC=10\cdot\dfrac{1}{2}=5\left(cm\right)\end{matrix}\right.\)
Vậy: DA=3cm; DC=5cm

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Vậy: BC=20cm

câu a bài 2 nhá
a) Gọi D là trung điểm BI => góc IDM = 45 độ
DM // IC ( đường trung bình )
=> góc BIC = 135 độ
=> 180 -1/2( góc B + góc C ) =135 độ
=> góc B + góc C = 90 độ
=> góc A = 90 độ

Xét hai tam giác ABC và tam giác HBA có
A = H = 90
B là góc chung
=> tam guacs ABC đồng dạng với tam giác HBA (g _ g) (1)
Xét hai tam giác ABC và tam giác HCA có
A= H = 90
C là góc chung
=> tam giác ABC ~ tam giác HAC ( g_ g) (2)
(1) =>\(\frac{AB}{BC}=\frac{BH}{BA}\)=> AB.AB = BH.BC => \(AB^2\)\(=BH.BC\)
(2) => \(\frac{AC}{BC}=\frac{CH}{AC}=AC.AC=BC.CH=AC^2=BC.CH\)
b ) Áp dụng định lý Py - ta - go vào tam giác ABC
\(BC^2=AC^2+AB^2\)= \(16^2+12^2\)= 400
=> BC = \(\sqrt{400}=20\)
từ tam giác ABC ~ HBA =>\(\frac{AB}{BH}=\frac{BC}{BA}< =>\frac{12}{BH}=\frac{20}{12}=>BH=\frac{12.12}{20}=7,2\)
từ tam giác ABC ~ HAC => \(\frac{AB}{HA}=\frac{BC}{AC}< =>\frac{12}{HC}=\frac{20}{16}=>HC=\frac{12.16}{20}=9,6\)
Áp dụng định lý Py - ta - go vào tam giác HBA
\(AH^2=AB^2-HB^2=12^2-7,2^2=9,6\)

a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)