Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác vuông BAC có ∠A = 90o
Áp dụng định lí Pitago, ta có:
BC2 = AB2 + AC2
= 62 + 82 = 36 + 64 = 100
⇒ BC = 10 (cm)
Kẻ IF ⊥ BC
Xét hai tam giác vuông IDB và IFB, ta có:
∠(IDB) = ∠(IFB) = 90o
∠(DBI) = ∠(FBI) (gt)
cạnh huyền BI chung
Suy ra: ΔIDB = ΔIFB (cạnh huyền, góc nhọn)
Suy ra: DB = FB (hai cạnh tương ứng) (4)
Xét hai tam giác vuông IEC và IFC, ta có:
∠(IEC) = ∠(IFC) = 90o
∠(ECI) = ∠(FCI) (gt)
cạnh huyền CI chung
Suy ra: ΔIEC = ΔIFC (cạnh huyền, góc nhọn)
Suy ra: CE = CF (hai cạnh tương ứng) (5)
Mà: AD + AE = AB - DB + AC - CE
Suy ra: AD + AE = AB + AC - (DB + CE) (6)
Từ (4), (5) và (6) suy ra: AD + AE = AB + AC - (FB + FC)
= AB + AC - BC = 6 + 8 - 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
Nên AD = AE = 4 : 2 = 2(cm).

a. Vì I là giao điểm các đường phân giác trong của B và C nên AI là tia phân giác của ∠A .
Suy ra: ID = IE (tính chất tia phân giác) (1)
Vì ΔADI vuông tại E có ∠(DAI) = 45o nên ΔADI vuông cân tại D
Suy ra: ID = IA (2)
Vì ΔAEI vuông tại E có ∠(EAI) = 45o nên ΔAEI vuông cân tại E
Suy ra: IE = AE (3)
Từ (1), (2) và (3) suy ra: AD = AE.
b. Tam giác vuông BAC có A = 90o
Áp dụng định lí Pitago, ta có:
BC2 = AB2 + AC2
= 62 + 82 = 36 + 64 = 100
⇒ BC = 10 (cm)
Kẻ IF ⊥ BC
Xét hai tam giác vuông IDB và IFB, ta có:
∠(IDB) = ∠(IFB) = 90o
∠(DBI) = ∠(FBI) (gt)
cạnh huyền BI chung
Suy ra: ΔIDB = ΔIFB (cạnh huyền, góc nhọn)
Suy ra: DB = FB (hai cạnh tương ứng) (4)
Xét hai tam giác vuông IEC và IFC, ta có:
∠(IEC) = ∠(IFC) = 90o
∠(ECI) = ∠(FCI) (gt)
cạnh huyền CI chung
Suy ra: ΔIEC = ΔIFC (cạnh huyền, góc nhọn)
Suy ra: CE = CF (hai cạnh tương ứng) (5)
Mà: AD + AE = AB - DB + AC - CE
Suy ra: AD + AE = AB + AC - (DB + CF) (6)
Từ (4), (5) và (6) suy ra: AD + AE = AB + AC - (FB + FC)
= AB + AC - BC = 6 + 8 - 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
Nên AD = AE = 4 : 2 = 2(cm).
a) AI là tai phân giác của góc A nên ID = IE. (1)
Các tam giác vuông ADI, AEI có DAIˆ=EAIˆ=45o nên là tam giác vuông cân, do đó AD = ID, AE = IE. (2)
Từ (1) và (2) suy ra AD = AE.
b) Áp dụng định lí Py-ta-go trong tam giác vuông ABC:
BC2 = AB2 + AC2 = 62 + 82
BC2 = 36 + 64 = 100
⇒BC=100−−−√=10(cm).
Kẻ IF ⊥ BC
Xét hai tam giác vuông IBD và IBF có:
BI: cạnh huyền chung
IBDˆ=IBFˆ (gt)
Vậy: ΔIBD=ΔIBF(ch−gn)
⇒ BD = BF (hai cạnh tương ứng)
Xét hai tam giác vuông ICE và ICF có:
CI: cạnh huyền chung
ICEˆ=ICFˆ(gt)
Vậy: ΔICE=ΔICF(ch−gn)
Suy ra: CE = CF (hai cạnh tương ứng)
Ta có: AB + AC - BC = AD + DB + AE + EC - BF - CF.
Do BD = BF, CE = CF nên:
AB + AC - BC = AD + AE
⇒ 6 + 8 - 10 = AD + AE
⇒ AD + AE = 4 (cm).
Theo câu a) ta có AD = AE nên AD = AE = 2cm.

a) AI là tai phân giác của góc A nên ID = IE. (1)
Các tam giác vuông ADI, AEI có DAI = EAI = 45o nên là tam giác vuông cân, do đó AD = ID, AE = IE. (2)
Từ (1) và (2) suy ra AD = AE.
b) Áp dụng định lí Py-ta-go trong tam giác vuông ABC:
BC2 = AB2 + AC2 = 62 + 82
BC2 = 36 + 64 = 100
⇒BC=\(\sqrt{100}\)=10(cm)
Kẻ IF ⊥ BC
Xét hai tam giác vuông IBD và IBF có:
BI: cạnh huyền chung
IBD = IBF (gt)
Vậy: ΔIBD=ΔIBF(ch−gn)
⇒ BD = BF (hai cạnh tương ứng)
Xét hai tam giác vuông ICE và ICF có:
CI: cạnh huyền chung
ICE = ICF(gt)
Vậy: ΔICE = ΔICF(ch−gn)
Suy ra: CE = CF (hai cạnh tương ứng)
Ta có: AB + AC - BC = AD + DB + AE + EC - BF - CF.
Do BD = BF, CE = CF nên:
AB + AC - BC = AD + AE
⇒ 6 + 8 - 10 = AD + AE
⇒ AD + AE = 4 (cm).
Theo câu a) ta có AD = AE nên AD = AE = 2cm.
Copy tại : https://h.vn/cau-hoi/cho-tam-giac-abc-vuong-tai-a-cac-tia-phan-giac-cua-cac-goc-b-va-c-cat-nhau-o-i-goi-d-va-e-la-chan-cac-duong-vuong-goc-ke-tu-i-den-ab-va-aca-chung.157922555778
Có gì vào link đó để xem hình vẽ và cách giải chi tiết
Hok tốt
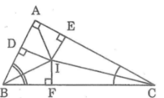
a) AI là tai phân giác của góc A nên ID = IE. (1)
Các tam giác vuông ADI, AEI có \(\widehat{DAI}=\widehat{EAI}=45^o\) nên là tam giác vuông cân, do đó AD = ID, AE = IE. (2)
Từ (1) và (2) suy ra AD = AE.
b) Áp dụng định lí Py-ta-go trong tam giác vuông ABC:
BC2 = AB2 + AC2 = 62 + 82
BC2 = 36 + 64 = 100
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\).
Kẻ IF \(\perp\) BC
Xét hai tam giác vuông IBD và IBF có:
BI: cạnh huyền chung
\(\widehat{IBD}=\widehat{IBF}\) (gt)
Vậy: \(\Delta IBD=\Delta IBF\left(ch-gn\right)\)
\(\Rightarrow\) BD = BF (hai cạnh tương ứng)
Xét hai tam giác vuông ICE và ICF có:
CI: cạnh huyền chung
\(\widehat{ICE}=\widehat{ICF}\left(gt\right)\)
Vậy: \(\Delta ICE=\Delta ICF\left(ch-gn\right)\)
Suy ra: CE = CF (hai cạnh tương ứng)
Ta có: AB + AC - BC = AD + DB + AE + EC - BF - CF.
Do BD = BF, CE = CF nên:
AB + AC - BC = AD + AE
\(\Rightarrow\) 6 + 8 - 10 = AD + AE
\(\Rightarrow\) AD + AE = 4 (cm).
Theo câu a) ta có AD = AE nên AD = AE = 2cm.
Hình tự vẽ nhé!!!
a) AI là tai phân giác của góc A nên ID = IE. (1)
Các tam giác vuông ADI, AEI có ˆDAI=ˆEAI=45oDAI^=EAI^=45o nên là tam giác vuông cân, do đó AD = ID, AE = IE. (2)
Từ (1) và (2) suy ra AD = AE.
b) Áp dụng định lí Py-ta-go trong tam giác vuông ABC:
BC2 = AB2 + AC2 = 62 + 82
BC2 = 36 + 64 = 100
⇒BC=√100=10(cm)⇒BC=100=10(cm).
Kẻ IF ⊥⊥ BC
Xét hai tam giác vuông IBD và IBF có:
BI: cạnh huyền chung
ˆIBD=ˆIBFIBD^=IBF^ (gt)
Vậy: ΔIBD=ΔIBF(ch−gn)ΔIBD=ΔIBF(ch−gn)
⇒⇒ BD = BF (hai cạnh tương ứng)
Xét hai tam giác vuông ICE và ICF có:
CI: cạnh huyền chung
ˆICE=ˆICF(gt)ICE^=ICF^(gt)
Vậy: ΔICE=ΔICF(ch−gn)ΔICE=ΔICF(ch−gn)
Suy ra: CE = CF (hai cạnh tương ứng)
Ta có: AB + AC - BC = AD + DB + AE + EC - BF - CF.
Do BD = BF, CE = CF nên:
AB + AC - BC = AD + AE
⇒⇒ 6 + 8 - 10 = AD + AE
⇒⇒ AD + AE = 4 (cm).
Theo câu a) ta có AD = AE nên AD = AE = 2cm.