Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác vuông ABC
Theo định lý Py - ta - go ta có :
AB2 + AC2 = BC2
=> 32 + AC2 = 52
=> 9 + AC2 = 25
=> AC2 = 16
=> AC = 4
Vậy AB < AC < BC
b. Xét tam giác BAM và tam giác BDM ta có :
BM chung
Góc BAM = góc BDM ( = 90 độ )
BA = BD ( gt)
=> tam giác BAM = tam giác BDM ( ch - cgv)
=> MA = MD ( hai cạnh tương ứng )
Xét tam giác AMN và tam giác DMC
góc AMN = góc DMC ( đối đỉnh )
MA = MD ( cmt)
góc MAN= góc MDC ( = 90 độ )
=> Tam giác AMN = tam giác DMC
=> MN = MC
=> Tam giác MNC cân

Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??

a: AC=căn 5^2-3^2=4cm
AB<AC<BC
=>góc C<góc B<góc A
b: xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
=>ΔBAM=ΔBDM
=>MA=MD
Xét ΔMAN vuông tại A và ΔMDC vuông tại D có
MA=MD
góc AMN=góc DMC
=>ΔMAN=ΔMDC
=>MN=MC
=>ΔMCN cân tại M

a: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BA=BD
BM chung
Do đó: ΔBAM=ΔBDM
Suy ra: MA=MD
Xét ΔAMN vuông tại A và ΔDMC vuông tại D có
MA=MD
\(\widehat{AMN}=\widehat{DMC}\)
Do đó: ΔAMN=ΔDMC
Suy ra: MN=MC
hay ΔMNC cân tại M
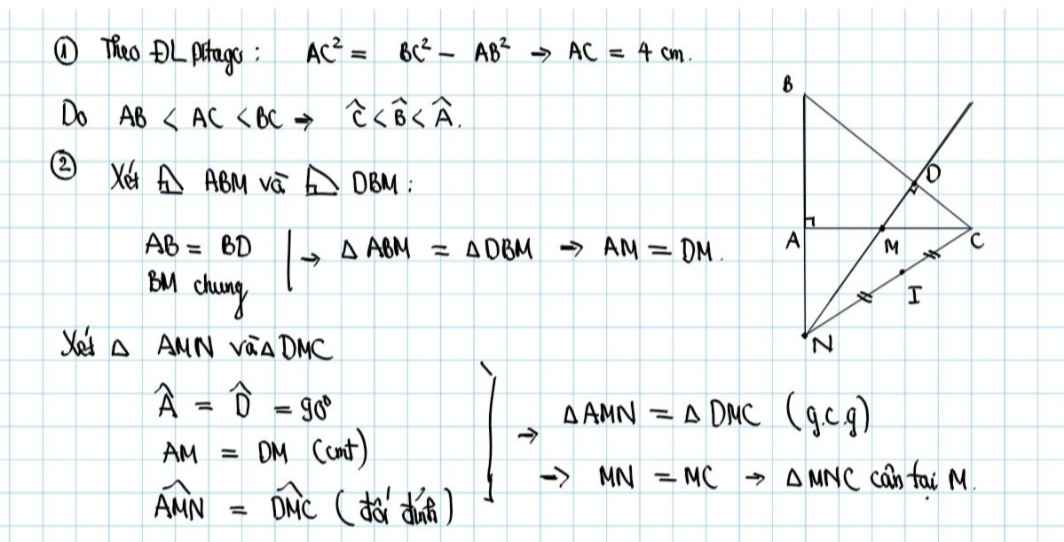

a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
=>ΔBAM=ΔBDM
=>MA=MD
c: Xet ΔMAN vuông tại Avà ΔMDC vuông tại D có
MA=MD
góc AMN=góc DMC
=>ΔMAN=ΔMDC
=>MN=MC
d: BN=BC
MN=MC
=>BM là trung trực của NC
=>B,M,I thẳng hàng