Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCAM vuông tại A và ΔCNM vuông tại N có
CM chung
góc ACM=góc NCM
=>ΔCAM=ΔCNM
b: Xét ΔMAK vuông tại A và ΔMNB vuông tại N có
MA=MN
góc AMK=góc NMB
=>ΔMAK=ΔMNB
=>MK=MB

1: Xét ΔCMA vuông tại M và ΔCNB vuông tại N có
CA=CB
\(\widehat{ACM}\) chung
Do đó: ΔCMA=ΔCNB
2: Xét ΔCAB có CN/CA=CM/CB
nên NM//BA

1: Xét ΔCAM vuông tại M và ΔCBN vuông tại N có
CA=CB
\(\widehat{ACM}\) chung
Do đó: ΔCAM=ΔCBN
Suy ra: CM=CN; AM=BN
Xét ΔCNK vuông tại N và ΔCMK vuông tại M có
CN=CM
CK chung
Do đó: ΔCNK=ΔCMK
Suy ra: \(\widehat{NCK}=\widehat{MCK}\)
hay CK là tia phân giác của góc ACB
2: Xét ΔCAB có CN/CA=CM/CB
nên MN//AB
3: AB=10cm
nên AD=DB=5cm
\(CD=\sqrt{12^2-5^2}=\sqrt{119}\left(cm\right)\)

1) Xét \(\Delta CAM\) vuông tại M và \(\Delta CBN\) vuông tại N:
\(\widehat{C}chung.\)
\(AC=BC\) (\(\Delta ABC\) cân tại C).
\(\Rightarrow\) \(\Delta CAM=\) \(\Delta CBN\left(ch-gn\right).\)
Xét \(\Delta ABC\) cân tại C:
BN là đường cao \(\left(BN\perp AC\right).\)
AM là đường cao \(\left(AM\perp BC\right).\)
K là giao điểm của AM; BN (gt).
\(\Rightarrow\) K là trực tâm.
\(\Rightarrow\) CK là đường cao từ đỉnh C.
\(\Rightarrow\) CK là tia phân giác \(\widehat{ACB}\) (Tính chất tam giác cân).
2) \(\Delta CAM=\) \(\Delta CBN\left(cmt\right).\)
\(\Rightarrow CM=CN\) (2 cạnh tương ứng).
\(\Rightarrow\) \(\Delta CNM\) cân tại C.
\(\Rightarrow\) \(\widehat{CNM}=\dfrac{180^o-\widehat{C}}{2}.\)
Mà \(\widehat{CAB}=\dfrac{180^o-\widehat{C}}{2}\) (\(\Delta ABC\) cân tại C).
\(\Rightarrow\) \(\widehat{CNM}=\widehat{CAB}.\)
\(\Rightarrow MN//AB\left(dhnb\right).\)
3) Xét \(\Delta ABC\) cân tại C:
CD là đường cao (cmt).
\(\Rightarrow\) CD là đường trung tuyến (Tính chất tam giác cân).
\(\Rightarrow\) D là trung điểm của AB.
\(\Rightarrow\) \(AD=\dfrac{1}{2}AB=\dfrac{1}{2}10=5\left(cm\right).\)
Xét \(\Delta ACD\) vuông tại D:
\(AC^2=CD^2+AD^2\left(Pytago\right).\\ \Rightarrow12^2=CD^2+5^2.\\ \Rightarrow CD^2=119.\\ \Rightarrow CD=\sqrt{119}\left(cm\right).\)

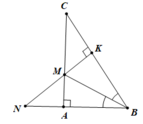
b. Xét ΔAMF và ΔKMC có:
AM = MK
∠(AMN) = ∠(KMC) (hai góc đối đỉnh)
⇒ ΔAMF = ΔKMC ( cạnh góc vuông – góc nhọn kề) (0.5 điểm)
⇒ MN = MC (hai cạnh tương ứng) (0.5 điểm)

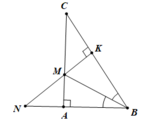
c. Do tam giác MKC vuông tại K nên MK < MC (0.5 điểm)
Mà MA = MK ⇒ MA < MC (0.5 điểm)

a) Xét tam giác ABD và tam giác HBD có :
góc ABD = góc HBD (BD là tia pg)
góc BAD = góc BHD=90 độ (gt)
BD là cạnh chung
=> Tam giác ABD = Tam giác HBD (CH-GN)
=> AD = DH ( 2 cạnh tương ứng )
b) Xét tam giác DHC có :
Góc DHC = 90 độ => DC là cạnh huyền => DC > DH
Ta lại có : AD=DH ( cm ở câu a )
=> DC>AD

Nếu tam giác ABC mà vuông tại A thì 2 tam giác ABM và ACM không thể bằng nhau đc
Mk nghĩ bn nên xem lại đề bài.
a: Xẻt ΔCAM vuông tại A và ΔCNM vuông tại N có
CM chung
góc ACM=góc NCM
=>ΔCAM=ΔCNM
b: Xét ΔMAK vuông tại A và ΔMNB vuông tại N có
MA=MN
góc AMK=góc NMB
=>ΔMAK=ΔMNB
=>MK=MB