Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tứ giác ABKC là hình thang vuông.
có AC vuông góc với AB, BK vuông góc góc AB
=> AC song song với BK (từ vuông góc đến song song)
=> tứ giác ACKB là hình thang và có góc CAB =900 (gt)
=> tứ giác ACKB là hình thang vuông
b) Theo câu a) ACKB là hình thang => AC song song với KB
=> góc CAK = góc AKB (so le trong)
Xét tam giác ABK và tam giác CHA có:
góc CAK = góc AKB (CM/trên)
và góc ABK = góc CHA (=900)
=> tam giác ABK đồng dạng với tam giác CHA (g-g)
\(\Rightarrow\dfrac{AB}{CH}=\dfrac{AK}{AC}\Rightarrow AB.AC=AK.CH\)
c) Xét tam giác CAH thì có góc CAH = 900 - góc ACH (1)
Xét tam giác ABC thì góc ABC = 900 - góc ACH (2)
Từ (1)(2)=. góc CAH = góc ABC
Xét tam giác CAH và tam giác ABH có:
góc CAH = góc HBA (CM/trên)
và góc CHA = góc AHB (=900)
=> tam giác CAH đồng dạng với tam giác ABH (g-g)
=> \(\dfrac{AH}{BH}=\dfrac{CH}{AH}\Rightarrow AH^2=CH.BH\)
d) Theo câu c) ta có \(AH^2=BH.CH\) thay số vào ta được:
\(AH^2=9.16=144\Rightarrow AH=12\left(cm\right)\)
Áp dụng định lí Py-ta-go vào tam giác AHB ta có:
\(AB^2=AH^2+HB^2=12^2+9^2=225\Rightarrow AB=15\left(cm\right)\)
hôm nào tớ thấy bn cũng có bài tập toàn bài tập dễ mà ko chịu làm ![]()

a: Xét tứ giác ABKC có BK//AC
nên ABKC là hình thang
mà góc CAB=90 độ
nên ABKC là hình thang vuông
b: Xét ΔaBK vuông tại B và ΔCHA vuông tại H có
góc BAK=góc HCA
Do đó ΔABK\(\sim\)ΔCHA
Suy ra: AB/CH=AK/AC
hay \(AB\cdot AC=AK\cdot CH\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
d: \(BC=BH+CH=25\left(cm\right)\)
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)

a, Xét tứ giác ABKC có: AC // BK ( cùng vuông góc vs AB)
=> Tứ giác ABKC là hình thang
mà \(\widehat{A}=90^o\)=> Tứ giác ABKC là hình thang vuông
b) Ta có: AC // BK => \(\widehat{AKB}=\widehat{CAH}\)( 2 góc so le trong)
Xét tam giác ABK và tam giác CHA có:
\(\widehat{ABK}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{AKB}=\widehat{CAH}\)(cmt)
=> Tam giác ABK đồng dạng với tam giác CHA
=> \(\frac{AB}{AK}=\frac{CH}{AC}\)=> AB. AC = AK.CH (đpcm)
c) Xét tam giác ABH và tam giác CAH có:
\(\widehat{AHB}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{BAH}=\widehat{ACH}\)( cùng phụ với góc HAC)
=> Tam giác ABH đồng dạng với tam giác CAH
=> \(\frac{AH}{BH}=\frac{CH}{AH}\)=> \(AH^2=BH.CH\)
d) Ta có: \(AH^2=BH.CH\)(cmc) => \(AH=\sqrt{BH.CH}=\sqrt{9.16}=12\)(cm)
Xét tam giác ABH vuông tại H, ta có: \(AB^2=BH^2+AH^2\)(định lý Pytago)
=> \(AB=\sqrt{BH^2+AH^2}=\sqrt{9^2+12^2}=15\)(cm)
Vậy AB = 15cm, AH = 12cm
Chúc bạn học tốt

A B C x K H
a) Xét Tứ giác ABKC có:
Bx vuông AB (gt)
AC vuông AB (gt)
=> Bx //AC.
=> Tứ giác ABKC là hình thang.
mà góc A= Góc B =90 đô.
Vậy hình thang ABKC là hình thang vuông.
b) Xét \(\Delta ABK\)vuông và \(\Delta CHA\)vuông :
Góc B = Góc H = 90 độ (gt)
Góc BAK = góc HCA ( cùng phụ góc HAC)
\(\Rightarrow\Delta ABK\infty\Delta CHA\)
c) Xét \(\Delta AHB\)vuông và \(\Delta CHA\)vuông:
Góc BHA = Góc AHC = 90 độ (gt)
Góc BAH = góc HCA (cùng phụ HAC)
\(\Rightarrow AHB\infty CHA\)
\(\Rightarrow\frac{AH}{CH}=\frac{HB}{AH}\Rightarrow AH^2=HC.HB\)
đề sai á: nếu HB.AC thì cac goc trong tam giác này ko đồng dạng.

B A C x K H
a) Ta có : \(AC//BK\left(cùng\text{ }\perp AB\right)\)
=> Tứ giác ABKC là hình thang
Mà \(\widehat{CAB}=90^0\left(gt\right)\)
=> Tứ giác ABKC là hình thang vuông.
b) Xét \(\Delta ABK\) và \(\Delta CHA\) có: \(\left\{{}\begin{matrix}\widehat{ABK}=\widehat{CHA}=90^0\left(gt\right)\\\widehat{KAB}=\widehat{ACH}\left(cùng\text{ }phụ\text{ }\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABK\sim\Delta CHA\left(g.g\right)\\ \Rightarrow\dfrac{AB}{CH}=\dfrac{AK}{AC}\\ \Rightarrow AB\cdot AC=CH\cdot AK\)
c) Xét \(\Delta AHC\) và \(\Delta BHA\) có: \(\left\{{}\begin{matrix}\widehat{AHC}=\widehat{BHA}=90^0\left(gt\right)\\\widehat{ACH}=\widehat{BAH}\left(cùng\text{ }phụ\text{ }\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHC\sim\Delta BHA\left(g.g\right)\\ \Rightarrow\dfrac{AH}{BH}=\dfrac{CH}{AH}\\ \Rightarrow AH^2=CH\cdot BH\)
\(\text{d) Ta có }:AH^2=CH\cdot BH=9\cdot16=144\left(cm\right)\\ \Rightarrow AH=12\left(cm\right)\\ AB=HB+HC=9+16=25\left(cm\right)\)

â ) Ta có : AC \(\perp\) AB ( tam giác ABC vuông tại A )
: BK \(\perp\)AB ( gt )
Do đo : AC // BK ( vì cùng vuông góc với AB )
Xét tứ giác ABKC , ta có :
\(\widehat{A}=90^O\) ( tam giác ABC vuông tại A )
\(\widehat{B}=90^O\left(gt\right)\)
AC // BK ( cmt )
Do đo : tứ giác ABKC là hình thang vuông
b ) Ta co : AC // BK ( cmt )
=> \(\widehat{K_1}=\widehat{A_2}\) ( hai góc so le trong của hai đường thẳng song song )
Xét :\(\Delta BAKva\Delta HCA,taco:\)
\(\widehat{B}=\widehat{H}=90^o\)
\(\widehat{K_1}=\widehat{A_2}\left(cmt\right)\)
Do do : \(\Delta BAK\) đồng dạng \(\Delta HCA\)( g - g )
= > \(\frac{AB}{AK}=\frac{CH}{AC}\)
=> AC . AC = AK . CH
c) CÂU NÀY CÓ 2 CÁCH NHA
Cach 1 )
Ta có : \(\widehat{A_1}+\widehat{B_1}=90^o\) ( tổng số đo hai góc nhọn trong tam giác vuông )
mà : \(\widehat{A_1}+\widehat{A_2}=90^o\) ( tia AK nằm giữa hai tia AB và AC )
nên \(\widehat{B_1}=\widehat{A_2}\) ( cung phụ vào góc \(\widehat{A_1}\) )
Xét : \(\Delta ABHva\Delta CAH,taco:\)
\(\widehat{H_1}=\widehat{H_2}=90^o\)
\(\widehat{B_1}=\widehat{A_2}=\left(cmt\right)\)
Do do : \(\Delta ABH\) đồng dạng \(\Delta CAH\left(g-g\right)\)
\(=>\frac{HC}{AH}=\frac{AH}{HB}\)
\(=>AH.AH=HB.HC\)
\(AH^2=9.16\)
\(AH^2=144\)
\(AH=\sqrt{144}=12cm\)
Áp dụng định lý pytago vào \(\Delta ABH\) vuông tại H
\(AB^2=AH^2+BH^2\)
\(AB=\sqrt{12^2+9^2}\)
\(AB=\sqrt{144+81}\)
\(AB=\sqrt{225}\)
\(AB=15cm\)
Cách 2 : ( của lớp 9 nha )
Ta có : BC = BH + HC = 9 + 16 = 25cm ( vì H nằm giữa B và C )
Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại A ( \(\widehat{A}=90^o;AH\perp BC\) )
\(AB^2=BH.BC\)
\(AB^2=9.25\)
\(AB^2=225\)
\(AB=\sqrt{225}=15cm\)
Áp dụng định lý pytago vào \(\Delta ABH\) vuông tại H
\(AH^2=AB^2-BH^2\)
\(AH^2=15^2-9^2\)
\(AH^2=225-81\)
\(AH^2=144\)
\(AH=\sqrt{144}=12cm\)
CÒN NHIỀU CÁCH NỮA NHA
OK CHÚC BẠN HỌC TỐT !!!!!
A B C K H
a) Ta có : \(KB\perp AB\)
\(AC\perp AB\)
\(\Rightarrow BK//AC\)
\(\Rightarrow\) tứ giác ABKC là hình thang
b) Ta có BK // AC
\(\Rightarrow\widehat{AKB}=\widehat{KAC}\)( so le trong )
Xét tam giác BAK và tam giác HCA có :
\(\widehat{AKB}=\widehat{KAC}\)
\(\widehat{ABK}=\widehat{AHC}\left(=90^o\right)\)
\(\Rightarrow\)tam giác BAK đồng dạng với tam giác HCA ( g-g ) (đpcm)
\(\Rightarrow\frac{BA}{HC}=\frac{AK}{CA}\)
\(\Leftrightarrow AB\times AC=AK\times CH\left(đpcm\right)\)
c) Xét tam giác ABC và tam giác HBA có :
\(\widehat{BAC}=\widehat{AHB}\left(=90^o\right)\)
Chung \(\widehat{ABC}\)
\(\Rightarrow\) tam giác ABC đồng dạng với tam giác HBA ( g-g )
\(\Rightarrow\frac{AB}{HB}=\frac{BC}{AB}\)
\(\Leftrightarrow AB^2=BC\times HB\)
\(\Leftrightarrow AB^2=\left(9+16\right)\times9\)
\(\Leftrightarrow AB^2=225\)
\(\Leftrightarrow AB=15\left(cm\right)\)
Áp dụng định lý Pi-ta-go cho tam giác ABH vuông tại H ta có :
\(BH^2+AH^2=AB^2\)
\(\Leftrightarrow9^2+AH^2=15^2\)
\(\Leftrightarrow81+AH^2=225\)
\(\Leftrightarrow AH=12\left(cm\right)\)
Vậy AB = 15 cm ; AH = 12 cm

A)Xet TG ABKC COS:
Bx VUONG GOC VOI AB(GT)
AC VUONG GOC VOI AB(GT)
=>BX//AC
=>TG ABKC LA HINH THANG(1)
MA GOC A=90 DO(2)
->TU (1) VA (2) =>TG ABKC LA HINH THANG VUONG
B)XET TAM GIAC ABK VA TAM GIAC CHA COS :
GOC B = GOC H =(90 DO )
GOC BAK=GOC HCA (VI CUNG PHU VOI GOC HAC)
=>TAM GIAC ABK DONG DANG VOI TAM GIAC CHA(G-G)
C)XET TAM GIAC AHC VA TAM GIAC AHB COS :
GOCS BHA=GOC AHC(=90 DO)
GOC BAH= GOC HCA(VI CUNG PHU VOI GOC HAC)
=>TAM GIAC AHC DONG DANG VOI TAM GIAC BHA(G-G)
=>\(\frac{AH}{HC}=\frac{BH}{AH}\)
=>AH^2=HB.HC(DPCM)
=>MAY MK K TRL DC CX HINH NEN PHAI TRL RIENG.SR NHES

A B C H K
a. Ta có: BK ⊥ AB
AB ⊥ AC
⇒ BK // AC
Suy ra: ABKC là hình thang
b.
Xét △ ABK và △CHA có:
Góc B = H = 90o
Góc AKB = CAH ( So le trong)
Do đó: △ABK ~ △CHA (g.g)
⇒ \(\dfrac{AB}{CH}=\dfrac{AK}{CA}\Rightarrow AB.AC=AK.CH\)
c.
Xét △HBA và △HAC có:
Góc H = 90o
Góc HBA = góc HAC ( cùng phụ góc C)
Do đó: △HBA~△HAC (g.g)
⇒ \(\dfrac{HB}{HA}=\dfrac{HA}{HC}\Rightarrow AH^2=HB.HC\)
d. Ta có: AH2 = HB.HC
⇒ AH2 = 9.16 = 144 (cm)
⇒ AH = 12 (cm)
Lại có: △ABH vuông tại H
⇒ AB2 = AH2 + BH2
\(\Rightarrow AB^2=12^2+9^2\)
⇒ AB2 = 225
⇒ AB = 15 (cm)
Vậy: AH = 12 cm; AB = 15 cm
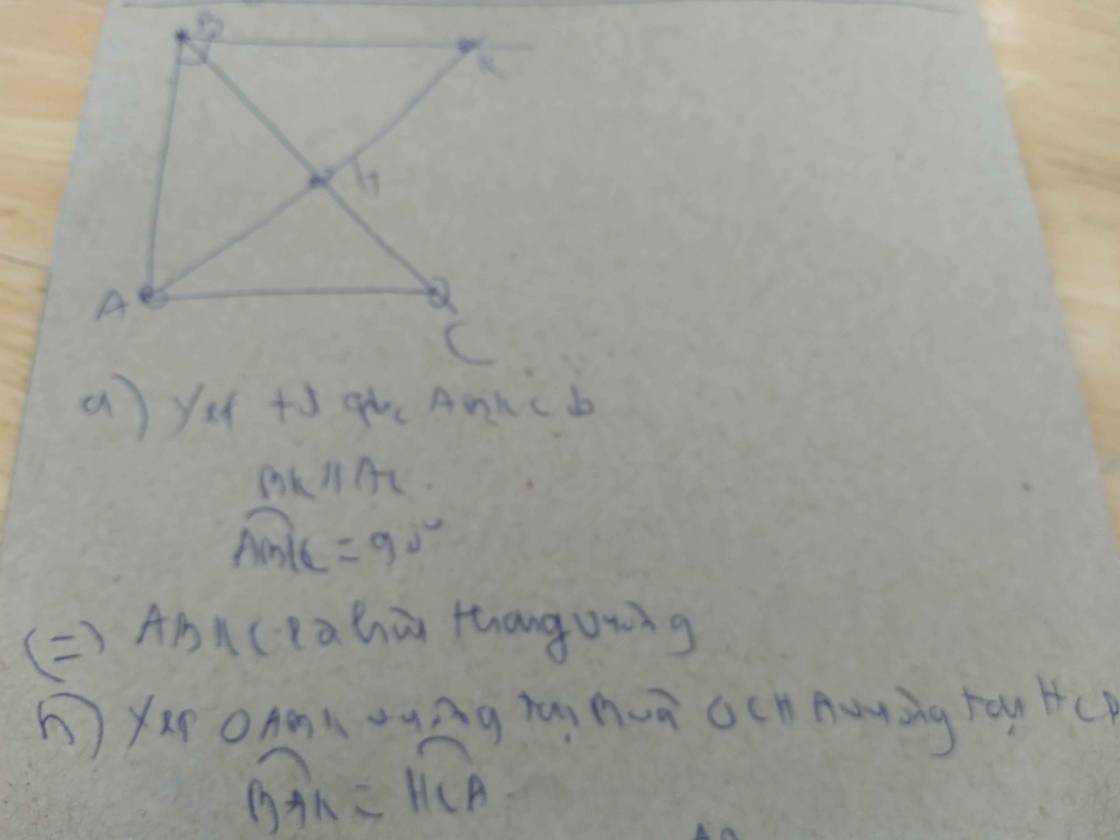

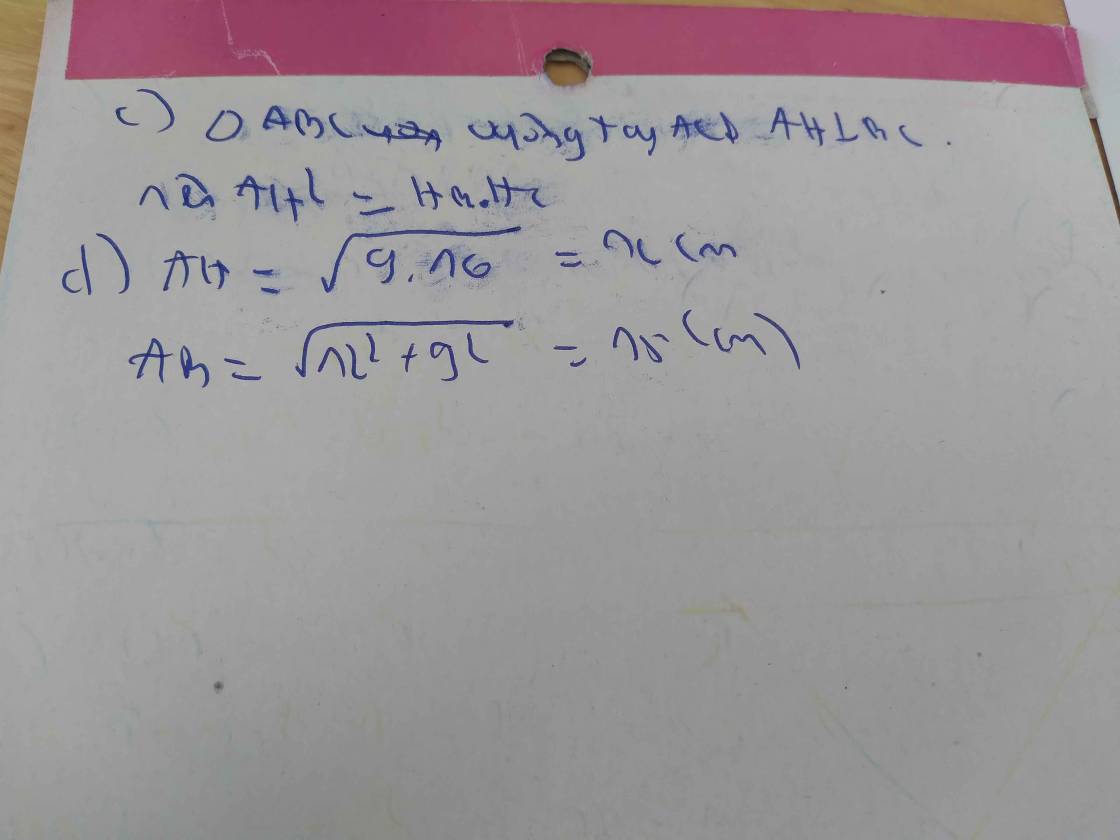
Xét tứ giác ABKC có:
\(B\chi\perp AB\) (gt)
\(AC\perp AB\) (gt)
\(\Rightarrow B\chi\text{//}AC\)
\(\Rightarrow\text{Tứ giác ABKC}\) là hình thang
mà \(\widehat{A}=\widehat{B}=\)\(90^0\)
Vậy hình thang ABKC là hình thang vuông
b) Xét ΔABK và ΔCHA có:
\(\widehat{ABK}=\widehat{CHA}=\)\(90^0\)
\(\widehat{BAK}=\widehat{HCA} \) ( cùng phụ với \(\widehat{HAC}\) )
\(\Rightarrow\text{ΔABK}\) \(\sim\)ΔCHA (gg)
\(\Rightarrow\dfrac{AB}{CH}=\dfrac{AK}{CA}\)
\(\Rightarrow AB.CA=AK.CH\)
c) Xét ΔAHB và ΔCHA có:
\(\widehat{AHB}=\widehat{CHA}=\)\(90^0\)
\(\widehat{BAH}=\widehat{HCA}\) ( cùng phụ với \(\widehat{HAC}\) )
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(gg\right)\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
\(\Rightarrow AH.AH=BH.CH\)
\(\Rightarrow AH^2=BH.CH\)
\(\Rightarrow AH^2=9.16\)
\(\Rightarrow AH=12\left(cm\right)\)
Xét \(\Delta AHB\) vuông tại H có:
\(AB^2=BH^2+HA^2\) ( Định lí Pitago)
\(\Rightarrow AB^2=9^2+12^2\)
\(\Rightarrow AB=\sqrt{225=15\left(cm\right)}\)