Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tai B
b: góc CAD+góc BAD=90 độ
góc HAD+góc BDA=90 độ
mà góc BAD=góc BDA
nên góc CAD=góc HAD
=>ĐPCM
c: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
góc HAD=góc EAD
=>ΔAHD=ΔAED
=>AH=AE; DH=DE
=>AD là trung trực của HE

a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD

a: Xét ΔBEA và ΔBED có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBEA=ΔBED

a) Xét ΔABM và ΔDBM có
BA=BD(gt)
\(\widehat{ABM}=\widehat{DBM}\)(BM là tia phân giác của \(\widehat{ABD}\))
BM chung
Do đó: ΔABM=ΔDBM(c-g-c)
Suy ra: \(\widehat{BAM}=\widehat{BDM}\)(hai góc tương ứng)
mà \(\widehat{BAM}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BDM}=90^0\)(đpcm)
b) Xét ΔABC vuông tại A có BC là cạnh huyền(BC là cạnh đối diện với \(\widehat{BAC}=90^0\))
nên BC là cạnh lớn nhất trong ΔABC(Định lí tam giác vuông)
Suy ra: BC>AC

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
ta có: BA=BE
=>B nằm trên trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>AK=EC và DK=DC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của KC(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng

a) Xét tam giác ABD và tam giác EBD:
+ AB = EB (gt).
+ BD chung.
+ \(\widehat{ABD}=\widehat{EBD}\) (BD là phân giác).
\(\Rightarrow\) Tam giác ABD = Tam giác EBD (c - g - c).
b) Tam giác ABD = Tam giác EBD (cmt).
\(\Rightarrow\) \(\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^o\) (Tam giác ABC vuông tại A).
\(\Rightarrow\) \(\widehat{BED}=90^o\)
c) Xét tam giác ABE: BA = BE (gt).
\(\Rightarrow\) Tam giác ABE cân tại B.
Mà BD là phân giác (gt).
\(\Rightarrow\) BD là đường cao (Tính chất tam giác cân).
\(\Rightarrow\) \(BD\perp AE.\)
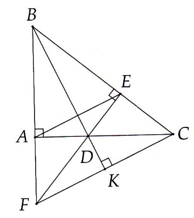


cho tam giác ABC cân tại A kể BD vuông góc với AC kề CE vuông góc với AB. Gọi y là giao điểm của BD và Ce
a)tam giác ABD= tam giác ACE
b)EY=YD
c)AY vuông BC
Xét ΔBAD và ΔBHD có
BA=BH
góc ABD=góc HBD
BD chung
Do đó: ΔBAD=ΔBHD