Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

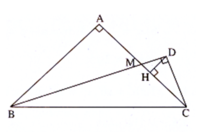
Theo câu a), từ AB = 2AM, suy ra HC = 2HD. Ta có HC < MC (h là chân đường cao hạ từ D của tam giác DCM vuông tại D) nên HC = 2HD < MC = AM < AH (do M nằm giữa A và H), vì thế 2HD không thể bằng AH. Khẳng định b) là sai.

a: Xét ΔHCD vuông tại H và ΔABM vuông tại A có
góc HCD=góc ABM
Do đó: ΔHCD đồng dạng với ΔABM
b: Khẳng định này sai

Chọn đáp án D

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 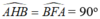
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 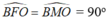
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
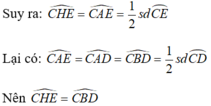
Và chúng ở vị trí so le trong suy ra: HE // BD

a) Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ACB}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{HCB}=90^0\)
Xét tứ giác HKBC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: HKBC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

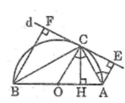
Ta có: AE // OC
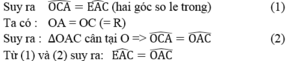
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE

Gọi tâm đường tròn đường kính AB là O
a) Xét (O) có AB là đường kính
nên O là trung điểm của AB
Ta có: OC⊥EF(EF là tiếp tuyến tại C của (O))
BF⊥FE(gt)
AE⊥FE(gt)
Do đó: AE//OC//BF(Định lí 1 từ vuông góc tới song song)
Xét tứ giác AEFB có AE//BF(cmt)
nên AEFB là hình thang có hai đáy là AE và BF(Định nghĩa hình thang)
Hình thang AEFB(AE//FB) có
O là trung điểm của AB(cmt)
OC//AE//BF(cmt)
Do đó: C là trung điểm của EF(Định lí 3 đường trung bình của hình thang)
hay CE=CF(đpcm)
b) Vì OC//AE(cmt)
nên \(\widehat{EAC}=\widehat{OCA}\)(hai góc so le trong)(1)
Xét ΔOAC có OA=OC(=R)
nên ΔOAC cân tại O(Định nghĩa tam giác cân)
⇒\(\widehat{OAC}=\widehat{OCA}\)(Hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{EAC}=\widehat{OAC}\)
hay \(\widehat{EAC}=\widehat{BAC}\)
mà tia AC nằm giữa hai tia AE,AB
nên AC là tia phân giác của \(\widehat{EAB}\)(đpcm)

Hai tam giác vuông HCD và DCM đồng dạng (có cùng góc nhọn tại C) mà
∆ DCM ∼ ∆ ABM (vì là hai tam giác vuông có ∠ (DMC) = ∠ (AMB), vậy ∆ HCD ∼ ∆ ABM. Khẳng định a) là đúng.