Question

[Dương Gia Huệ]

Cho tam giác ABC vuông cân tại A, có AH là đường cao. Gọi M là một điểm bất kì trên cạnh BC, I và K lần lượt là hình chiếu vuông góc của M trên AB, AC. Chứng minh tam giác IHK vuông cân.

Answer 1

[tth_new]

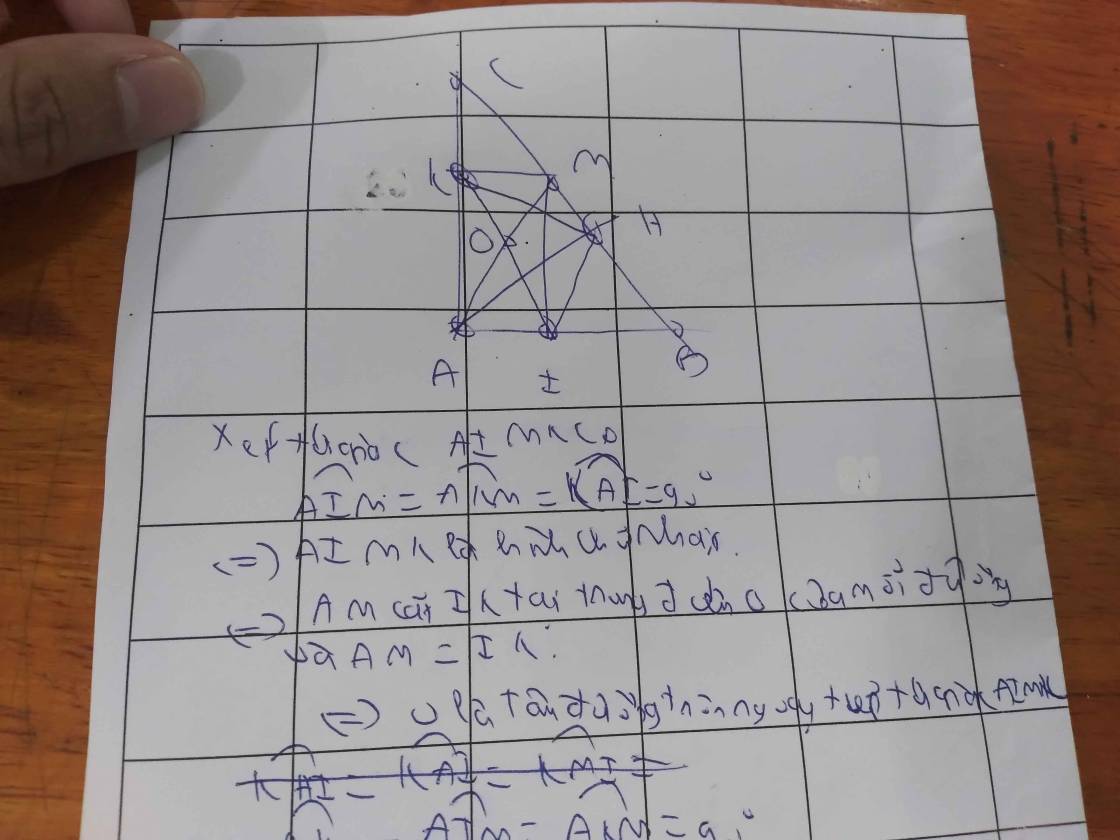
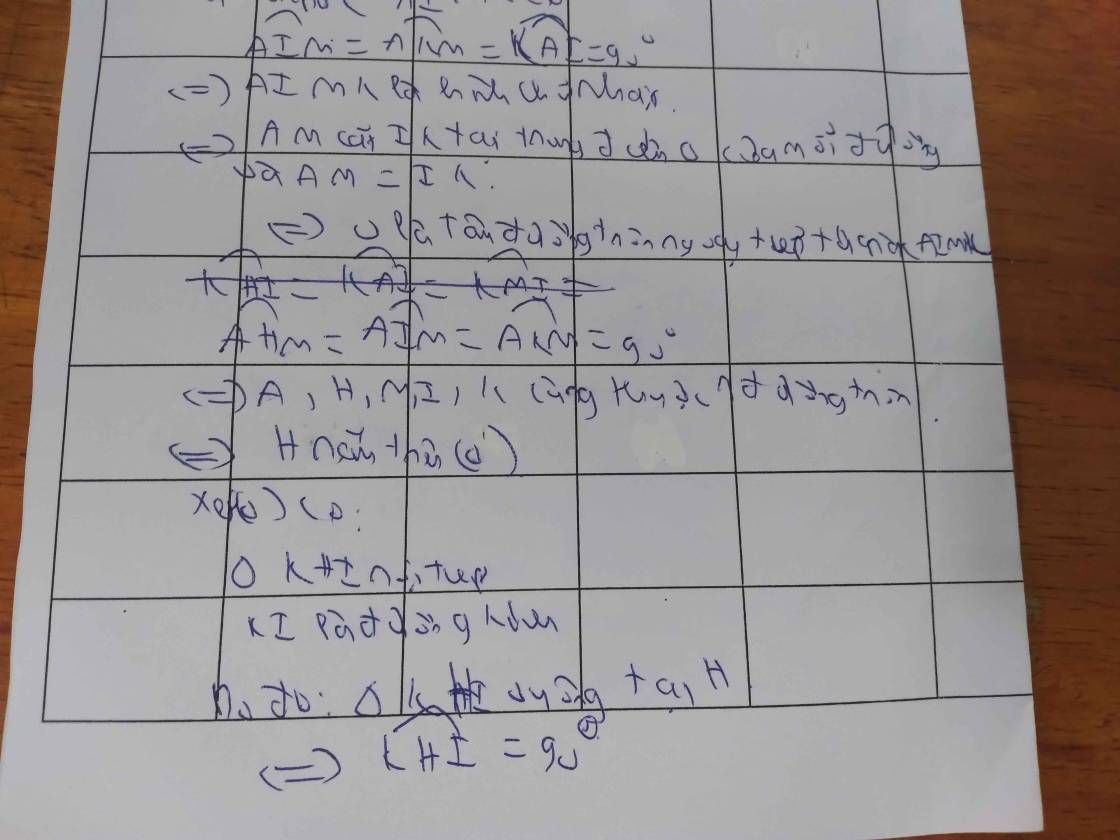
Không mất tính tổng quát, ta xét M thuộc HC (trường hợp M thuộc HB tương tự)

Tam giác ABC vuông tại A có đường cao AH xuất phát từ đỉnh A nên \(AH=\frac{1}{2}BC\) (1) và AH cũng là đường trung tuyến \(\Rightarrow HC=HB=\frac{1}{2}BC\) (2) và đường phân giác => ^CAH = ^BAH. Từ (1) và (2) suy ra \(\Delta\)AHC vuông cân tại H. Từ đó 

AH = HC và ^ACH = ^HAC = ^BAH. Tới đây tìm cách chứng minh AI = CK(mình chưa biết làm đâu:v). Từ đó suy ra \(\Delta\)HIA = \(\Delta\)HKC. Suy ra ^AHI = ^CHK suy ra ^IHK = ^IHA + ^AHK = ^CHK + ^AHK = 90^o => \(\Delta\)IHK vuông tại H (3)

Mặt khác từ  \(\Delta\)HIA = \(\Delta\)HKC suy ra HI =HK suy ra  \(\Delta\)IHK cân tại H (4)

Từ (3) và (4) suy ra đpcm.

P/s: Ko chắc, bác zZz Cool Kid zZz check giúp:v

Answer 2

[Huyền Nhi]

làm đoạn tth thiếu nhé:

cm AI=CK

t/g ABC vuông cân tại A => ABC^=45 độ

t/g BIM có I^=90 độ mà ABC^=45 độ => BMI^=45 độ

=> t/g BIM vuông cân tại I => BI=IM 

Mà tứ giác BIAK có I^=A^=K^=90 độ => tứ giác BIAK là HCN => IM=AK=BI

Mà AB=AC

=> AB-BI=AC-AK

=>  AI=CK