Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh tứ giác AEDF là hình thoi
Þ EF là phân giác của A E D ^
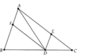

Hình tự vẽ nha bạn
Vì AD là đường phân giác của góc A
=> \(\widehat{BAD}=\widehat{DAE}\)
Vì AB//ED =>\(\widehat{BAD}=\widehat{EDA}\)(2 góc so le trong)
Mà góc BAD=góc DAE=> \(\widehat{DAE}=\widehat{EDA}\)
=> tam giác EAD cân tại E
=>EA=ED
Ta có: AB//ED cắt FE//BC => BF=ED(theo tính chất đoạn chắn)
Mà EA=ED=> AE=BF(=ED)

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
Hình bình hành AEDF có AD là phân giác của góc FAE
nên AEDF là hình thoi
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{CD}{DB}=\dfrac{AC}{AB}\left(1\right)\)
Xét ΔABC có DE//AB
nên \(\dfrac{CD}{DB}=\dfrac{CE}{EA}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AC}{AB}=\dfrac{EC}{EA}\)
=>\(AC\cdot AE=AB\cdot EC\)

zì \(\hept{\begin{cases}MD//AE\\ME//AD\end{cases}}\)
=> tứ giác ADME là hbh
=>\(\hept{\begin{cases}AD=ME\\AE=MD\end{cases}}\)
=>\(\frac{AD}{AB}=\frac{ME}{AB}\)
mà ME//AB
=>\(\frac{ME}{AB}=\frac{CE}{AC}=>\frac{AD}{AB}=\frac{CE}{AC}\)
=>\(\frac{AD}{AB}+\frac{AE}{AC}=\frac{CE}{AC}+\frac{AE}{AC}=\frac{CE+AE}{AC}=\frac{AC}{AC}=1\left(dpcm\right)\)

Xét \(\Delta\text{A}BC\)có :
\(ED//\text{A}C\left(gt\right)\)
\(\Rightarrow\frac{BE}{\text{A}B}=\frac{DE}{\text{A}C}\)
\(\Rightarrow\frac{BE}{ED}=\frac{\text{A}B}{\text{A}C}(1)\)
Có : AD là phân giác góc \(B\text{A}C\)
=> góc \(B\text{A}D\)= góc \(C\text{A}D\)
Có : \(ED//\text{A}C\left(gt\right)\)
=> góc \(\text{A}DE\)= góc \(C\text{A}D\)
mà góc \(B\text{A}D\)= góc \(C\text{A}D\) ( cmt)
=> góc \(\text{A}DE\)= góc \(B\text{A}D\)
=> \(\Delta ED\text{A}\) cân tại E
=> \(ED=E\text{A}\)
Cộng mỗi vế của (1) với 1, ta có :
\(1+\frac{\text{A}B}{\text{A}C}=\frac{BE}{ED}+1\)
=>\(\frac{\text{A}B}{\text{A}B}+\frac{\text{A}B}{\text{A}C}=\frac{BE}{ED}+\frac{ED}{ED}\)
mà \(ED=E\text{A}\left(cmt\right)\)
=>\(\frac{\text{A}B}{\text{A}B}+\frac{\text{A}B}{\text{A}C}=\frac{BE}{ED}+\frac{E\text{A}}{ED}\)
=>\(\frac{\text{A}B}{\text{A}B}+\frac{\text{A}B}{\text{A}C}=\frac{\text{A}B}{ED}\)
=>\(\frac{1}{\text{A}B}+\frac{1}{\text{A}C}=\frac{1}{ED}\)
mà \(ED=E\text{A}\left(cmt\right)\)
=> \(\frac{1}{\text{A}B}+\frac{1}{\text{A}C}=\frac{1}{E\text{A}}\left(đpcm\right)\)