Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác AB'C' và tgiac ABC có
AB'=AB (gt)
AC'=AC (gt)
Góc BAC=B'AC'
Vậy 2 tam giác = nhau(c.g.c)
Suy ra: B'C'A=ABC
Mà 2 góc này nằm ở vị trí so le trong
Suy ra: B'C' SONG SONG BC
Vậy tứ giác B'C'CB là hình thang

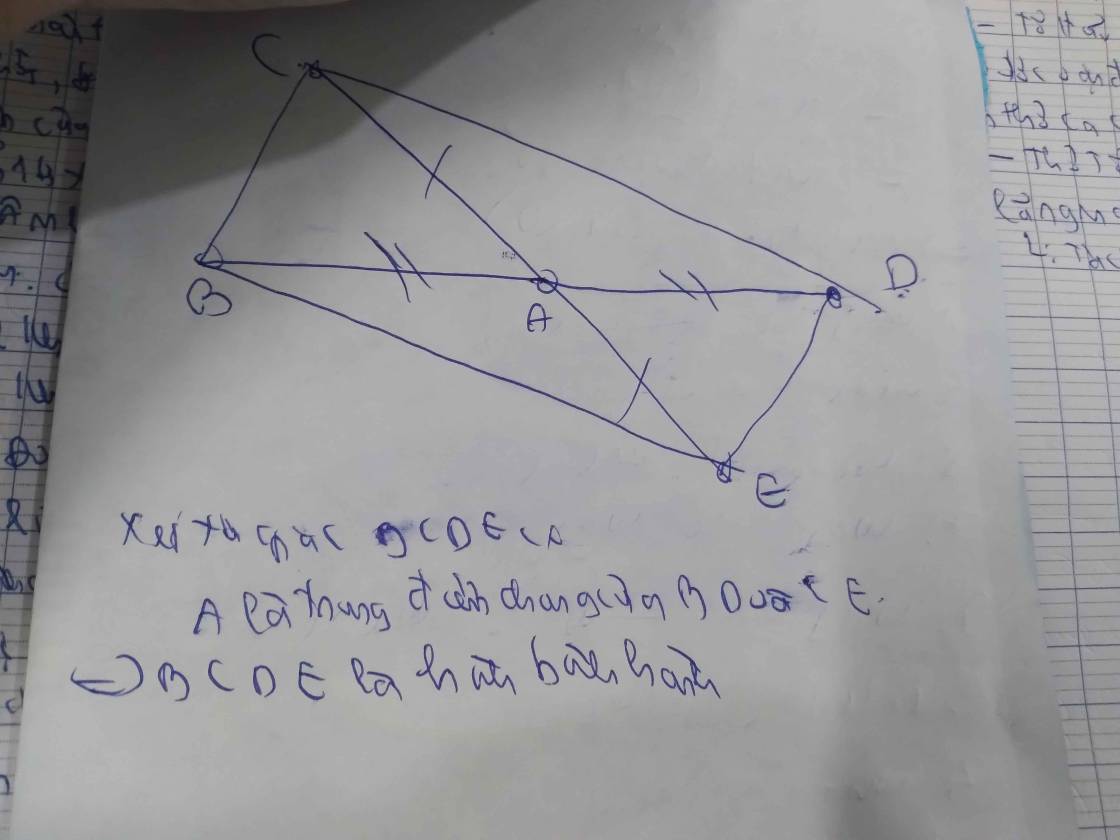
Vì \(\widehat{B1}=\widehat{E1}\)( sole trong )
\(\Rightarrow BD//EC\)
=> BECD là hình thang
Mà \(AE=AC\left(GT\right)\)
=> \(\Delta EAC\)cân
=> \(\widehat{E}=\widehat{C}\)
=> BECD là hình thang cân

bn vào Link này xem thử nhé :
Cho tam giác đều ABC. Trên tia đối tia AB lấy điểm D và trên tia đối tia AC lấy điểm E sao cho AD = AE. Gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng BE,AD,AC,ABa) Chứng minh rằng tứ giác BCDE là hình thang cânb) Chứng minh rằng tứ giác CNEQ là hình thangc) Tam giác MNP là tam giác đề - Tìm với Google
Hok tốt
# EllyNguyen #

mình mới học dến bài hình thang thôi.hình thang cân mình chưa học nhé

Bạn kham khảo nha:
Cho tam giác đều ABC. Trên tia đối tia AB lấy điểm D và ... - Online Math
Vì \(\widehat{B_1}=\widehat{E_1}\)( sole trong)
\(\Rightarrow BD//EC\)
=> BECD là hình thang
Mà \(AE=AC\left(GT\right)\)
\(\Rightarrow\Delta EAC\)Cân
\(\Rightarrow\widehat{E}=\widehat{C}\)
=> BECD là hình thang cân.