Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử \(\vec{AB} = \mathbf{a}\), \(\vec{AD} = \mathbf{b}\), và \(\vec{AM} = \frac{1}{2}\vec{AC}\).
Vì \(ABCD\) là hình thoi, nên \(\vec{AB} = \vec{DC} = -\vec{CB}\).
Do đó, \(\vec{CB} = -\mathbf{a}\) và \(\vec{AM} = \frac{1}{2}(\vec{AC}) = \frac{1}{2}(\vec{AD} + \vec{DC}) = \frac{1}{2}(\mathbf{b} - \mathbf{a})\).
Bây giờ, tính tích vô hướng \(\vec{MA} \times \vec{CB}\):
\[\vec{MA} \times \vec{CB} = \frac{1}{2}(\mathbf{b} - \mathbf{a}) \times (-\mathbf{a})\]
Sử dụng tích vô hướng của vecto, ta có:
\[\vec{MA} \times \vec{CB} = \frac{1}{2}(\mathbf{b} \times (-\mathbf{a})) - \frac{1}{2}(\mathbf{a} \times (-\mathbf{a})\]
Với \(\mathbf{b} \times (-\mathbf{a}) = -(\mathbf{a} \times \mathbf{b})\), và \(\mathbf{a} \times (-\mathbf{a}) = -\|\mathbf{a}\|^2\), ta có:
\[\vec{MA} \times \vec{CB} = \frac{1}{2}(\mathbf{a} \times \mathbf{b}) + \frac{1}{2}\|\mathbf{a}\|^2\]
Nếu bạn có thông tin cụ thể về \(\mathbf{a}\) và \(\mathbf{b}\), bạn có thể tính toán giá trị này.

b: AM=1/3AC
=>\(S_{ABM}=\dfrac{1}{3}\cdot S_{ABC}\)
=>\(S_{ABC}=54\left(cm^2\right)\)

a: AM=MN=NC
=>S BAM=S BNM =S BNC
b: S ABC=3/2*18=27cm2

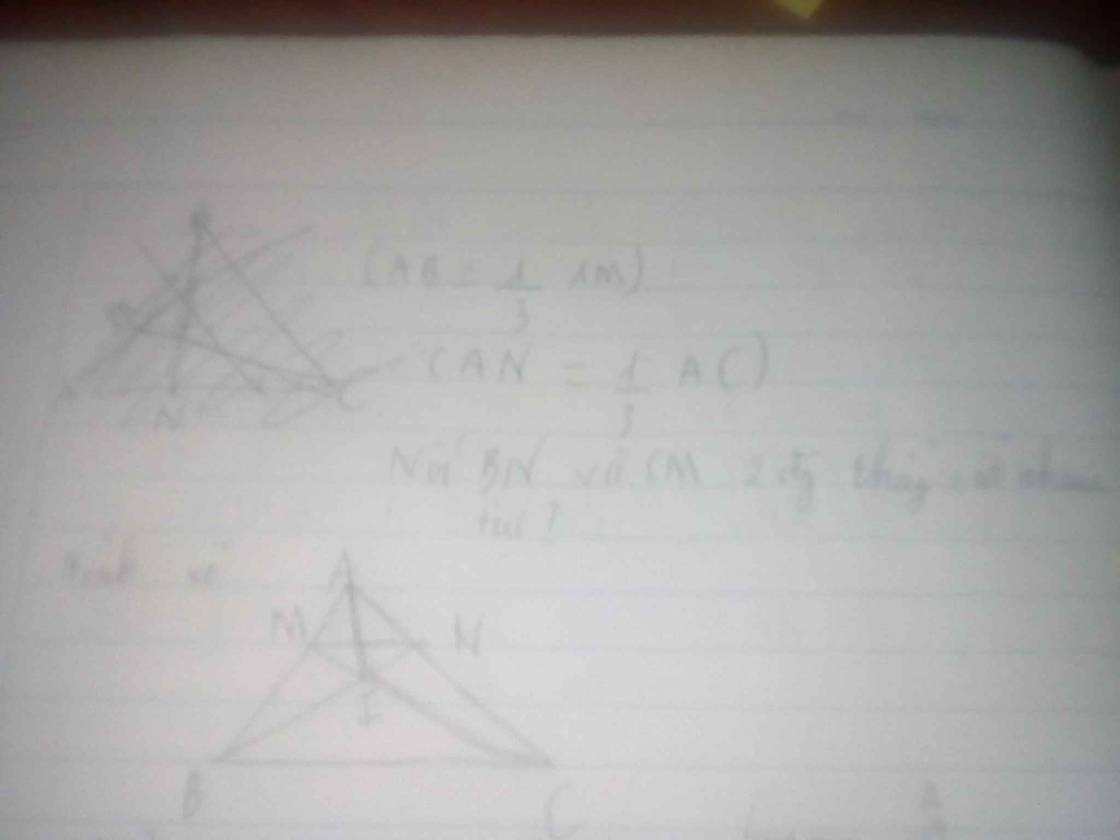 cái này là hình vẽ nhé!
cái này là hình vẽ nhé!
a, Tam giác AIB và tam giác ABC có chung chiều cao hạ từ B xuống AC, đáy AN = 1/3 đáy AC.
=> SAIB = 1/3 x S ABC.
Tam giác AIC và ABC có chiều cao hạ từ C xuống ABC, đáy AM = 1/3 đáy ABC.
=> SAIC = 1/3 x SABC.
=> SAIB = SAIC ( Vì cùng bằng = 1/3 SABC)
câu b thì bạn chưa nói rõ nên mình đưa bạn bản mẫu là tứ giác và 90cm2 nhé!
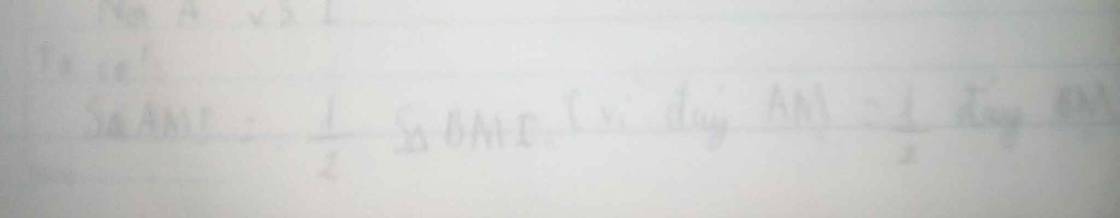 Ta có :
Ta có :
SAMI = 1/2 SƠMI ( vì đáy ÂM = 1/2 đáy BM)
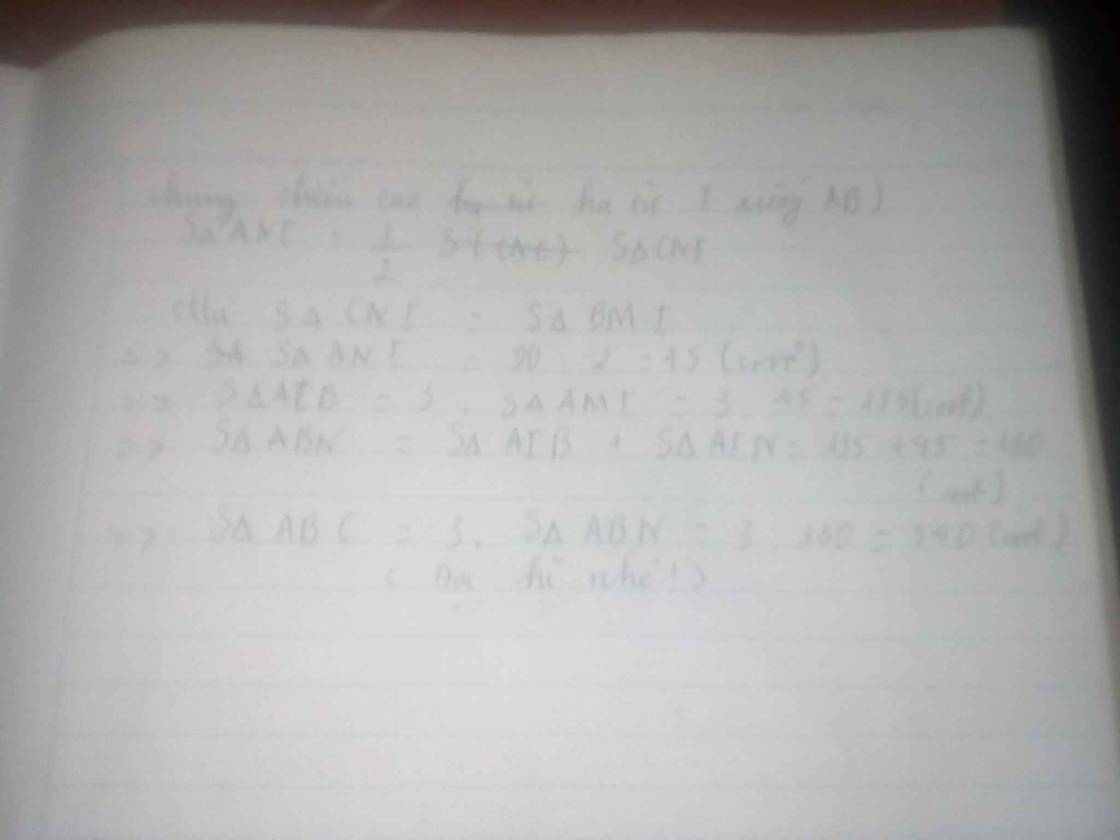 bạn thông cảm vì máy chụp hơi kém nhé!
bạn thông cảm vì máy chụp hơi kém nhé!