Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta giải như sau :
a) 1. Góc ACF + Góc BAC = 90 độ ; Góc EBA + BAC = 90 độ => Góc ACF = Góc EBA (cùng phu với Góc BAC)
Mà ACF và EBA là hai góc chắn cung EF của tứ giác EFBC và bằng nhau
=> Tứ giác EFBC nội tiếp.
2. Ta có : BE vuông góc với AC tại E ; CK vuông góc với AC tại C (Vì góc ACK chắn nửa cung tròn đường kính AK)
=> BE // CK (1)
Tương tự ta cũng có : BK // CF (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (dhnb)
b) Vì tứ giác BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC => M cũng là trung điểm HK
Xét tam giác AHK có AM và HO lần lượt là hai đường trung tuyến ( AO = OK ; HM = MK) cắt nhau tại I
=> I là trọng tâm tam giác AHK
Lại có AM là đường trung tuyến tam giác ABC và I thuộc AM => I là trọng tâm tam giác ABC
c) Mình chưa nghĩ ra :))
giải như sau :
a) 1. Góc ACF + Góc BAC = 90 độ ; Góc EBA + BAC = 90 độ => Góc ACF = Góc EBA (cùng phu với Góc BAC)
Mà ACF và EBA là hai góc chắn cung EF của tứ giác EFBC và bằng nhau
=> Tứ giác EFBC nội tiếp.
2. Ta có : BE vuông góc với AC tại E ; CK vuông góc với AC tại C (Vì góc ACK chắn nửa cung tròn đường kính AK)
=> BE // CK (1)
Tương tự ta cũng có : BK // CF (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (dhnb)
b) Vì tứ giác BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC => M cũng là trung điểm HK
Xét tam giác AHK có AM và HO lần lượt là hai đường trung tuyến ( AO = OK ; HM = MK) cắt nhau tại I
=> I là trọng tâm tam giác AHK
Lại có AM là đường trung tuyến tam giác ABC và I thuộc AM => I là trọng tâm tam giác ABC

a) Bổ đề: Xét tam giác ABC cân tại A, một điểm M bất kì sao cho ^AMB = ^AMC. Khi đó MB = MC.
Bổ đề chứng minh rất đơn giản, không trình bày ở đây.
Áp dụng vào bài toán: Vì E là điểm chính giữa (BC nên EB = EC = ED => \(\Delta\)BED cân tại E
Ta có ^BAE = ^CAE (2 góc nội tiếp chắn hai cung bằng nhau) hay ^BAE = ^DAE
Áp dụng bổ đề vào \(\Delta\)BED ta được AB = AD. Khi đó AE là trung trực của BD => AE vuông góc BD
Lại có \(\Delta\)BAD ~ \(\Delta\)CFD (g.g). Mà AB = AD nên FD =FC. Từ đó EF vuông góc DC
Xét \(\Delta\)AEF có FD vuông góc AE (cmt), AD vuông góc EF (cmt) => D là trực tâm \(\Delta\)AEF (đpcm).
b) Gọi DN cắt EC tại I. Ta dễ thấy ^MDI = ^MDN = ^MBN = ^MBC = ^MEC = ^MEI
Suy ra bốn điểm D,E,M,I cùng thuộc một đường tròn => ^EMD = ^EID = 900
Nếu ta gọi MD cắt cung lớn BC của (O) tại S thì ^EMS chắn nửa (O) hay ES là đường kính của (O)
Mà E là điểm chính giữa cung nhỏ BC nên S là điểm chính giữa cung lớn BC
Do đó S là điểm cố định (Vì B,C cố định). Vậy MD luôn đi qua S cố định (đpcm).

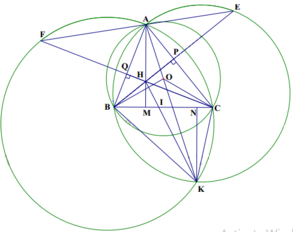
Ta có BOC=120o ;BKC =60o suy ra BOC +BKC =1800 nên tứ giác BOCK nội tiếp đường tròn.
Ta có OB=OC=R suy ra OB= OC=> BKO= CKO hay KO là phân giác góc BKC theo phần (a) KA

a) Vì tứ giác BFEC nội tiếp nên \(\widehat{PFB}=\widehat{ACB}=\widehat{PBF}\) suy ra \(PF=PB\)
Suy ra \(MP\perp AB\) vì MP là trung trực của BF. Do đó \(MP||CF\). Tương tự \(MQ||BE\)
b) Dễ thấy M,I,J đều nằm trên trung trực của EF cho nên chúng thẳng hàng. Vậy IJ luôn đi qua M cố định.
c) Gọi FK cắt AD tại T ta có \(FK\perp AD\) tại T. Theo hệ thức lượng \(IE^2=IF^2=IT.IL\)
Suy ra \(\Delta TIE~\Delta EIL\). Lại dễ có \(EI\perp EM\), suy ra ITKE nội tiếp
Do vậy \(\widehat{ILE}=\widehat{IET}=\widehat{IKT}=90^0-\widehat{LIK}\). Vậy \(IK\perp EL.\)