Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔBAC có
BN là đường cao ứng với cạnh huyền AC
CM là đường cao ứng với cạnh huyền AB
BN cắt CM tại H
Do đó: AH⊥BC

a, Vì \(\widehat{BMC}=\widehat{BNC}=90^0\) (góc nt chắn nửa đg tròn) nên BN,CM là đường cao tam giác ABC
Do đó H là trực tâm tam giác ABC
Vậy AH là đường cao thứ 3 hay AH⊥BC tại D
b, \(OC=ON\Rightarrow\widehat{ONC}=\widehat{OCN}\)
Mà NE là trung tuyến ứng cạnh huyền tg AHN nên \(NE=EH\)
\(\Rightarrow\widehat{ANE}=\widehat{EAN}\)
\(\Rightarrow\widehat{ANE}+\widehat{ONC}=\widehat{OCN}+\widehat{EAN}=90^0\left(\Delta ADC\perp D\right)\\ \Rightarrow\widehat{ENO}=180^0-\left(\widehat{ANE}+\widehat{ONC}\right)=90^0\\ \Rightarrow EN\perp ON\left(đpcm\right)\)

a:
góc BDC=góc BEC=1/2*sđ cung BC=90 độ
=>CD vuông góc AB và BE vuông góc AC
Xét ΔABC có
CD,BE là đường cao
CD cắt BE tại H
=>H là trực tâm
=>AH vuông góc BC
b: góc AEH+góc ADH=180 độ
=>AEHD nội tiếp đường tròn đường kính AH
=>I là trung điểm của AH
c: góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>O là trung điểm của BC
d: ID=IE
OD=OE
=>OI là trung trực của DE
=>OI vuông góc DE

a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
=>CF vuông góc AB
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE vuông góc AC
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm
=>AH vuông góc BC tại D
b: Xét tứ giác AFHE có
góc AFH+góc AEH=90+90=180 độ
=>AFHE nội tiếp đường tròn đường kính AH
I là trung điẻm của AH
c:
Xét tứ giác BFHD có
góc BFH+góc BDH=180 độ
=>BFHD nội tiếp
=>góc DFH=góc DBH=góc EBC
góc IFD=góc IFH+góc DFH
=góc IHF+góc EBC
=góc DHC+góc EBC
=90 độ-góc FCB+góc EBC
=90 độ
=>IF là tiếp tuyến của (O)
Xét ΔIFD và ΔIED có
IF=IE
FD=ED
ID chung
=>ΔIFD=ΔIED
=>góc IED=góc IFD=90 độ
=>IE là tiếp tuyến của (O)

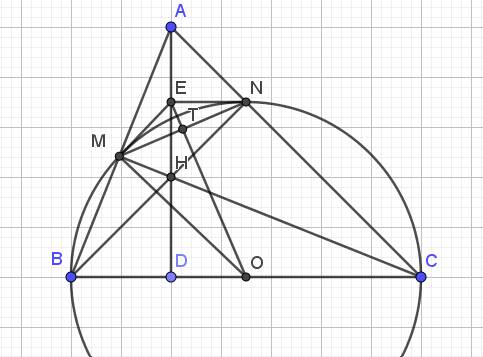
Lời giải:
a. Ta có:
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó;ΔBEC vuông tại E
=>CE\(\perp\)BE tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó;ΔBDC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Xét tứ giác AEHD có \(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
=>AEHD là tứ giác nội tiếp đường tròn đường kính AH
=>A,E,H,D cùng nằm trên đường tròn đường kính AH
c: I là tâm của đường tròn đi qua 4 điểm A,E,H,D
=>I là trung điểm của AH
Gọi giao điểm của AH với BC là M
AH\(\perp\)BC
nên AH\(\perp\)BC tại M
\(\widehat{BHM}=\widehat{IHD}\)
mà \(\widehat{IHD}=\widehat{IDH}\)(ID=IH)
nên \(\widehat{BHM}=\widehat{IDH}\)
mà \(\widehat{BHM}=\widehat{BCD}\left(=90^0-\widehat{HBM}\right)\)
nên \(\widehat{IDH}=\widehat{BCD}\)
OB=OD
=>ΔODB cân tại O
=>\(\widehat{OBD}=\widehat{ODB}\)
=>\(\widehat{ODH}=\widehat{DBC}\)
\(\widehat{IDO}=\widehat{IDH}+\widehat{ODH}\)
\(=\widehat{DBC}+\widehat{DCB}\)
\(=90^0\)
=>ID\(\perp\)DO

a) Ta có: \(\widehat{AMO}=\widehat{ADO}=\widehat{ANO}=90^o\) nên \(M,N,D\) cùng nhìn \(AO\) dưới một góc vuông suy ra \(M,D,O,N,A\) cùng thuộc một đường tròn.
b) Gọi \(F\) là giao điểm của \(AC\) và đường tròn \(\left(O\right)\).
\(\Delta ANF\sim\Delta ACN\left(g.g\right)\) suy ra \(AN^2=AC.AF\).
Xét tam giác \(AHN\) và tam giác \(AND\):
\(\widehat{HAN}=\widehat{NAD}\) (góc chung)
\(\widehat{ANH}=\widehat{ADN}\) (vì \(AMDON\) nội tiếp, \(\widehat{ANH},\widehat{ADN}\) chắn hai cung \(\stackrel\frown{AM},\stackrel\frown{AN}\) mà \(AM=AN\))
\(\Rightarrow\Delta AHN\sim\Delta AND\left(g.g\right)\)
suy ra \(AN^2=AH.AD\)
suy ra \(AC.AF=AH.AD\)
\(\Rightarrow\Delta AFH\sim\Delta ADC\left(c.g.c\right)\Rightarrow\widehat{AFH}=\widehat{ADC}=90^o\)
suy ra \(\widehat{HFC}=90^o\) mà \(\widehat{BFC}=90^o\) (do \(F\) thuộc đường tròn \(\left(O\right)\))
suy ra \(B,H,F\) thẳng hàng do đó \(BH\) vuông góc với \(AC\).
Tam giác \(ABC\) có hai đường cao \(AD,BF\) cắt nhau tại \(H\) suy ra \(H\) là trực tâm tam giác \(ABC\).

Sửa đề: BF và CE cắt nhau tại H
a) Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C\(\in\)(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
\(\Leftrightarrow CE\perp BE\)
\(\Leftrightarrow CE\perp AB\)
\(\Leftrightarrow\widehat{AEC}=90^0\)
hay \(\widehat{AEH}=90^0\)
Xét (O) có
ΔBFC nội tiếp đường tròn(B,F,C\(\in\)(O))
BC là đường kính(gt)
Do đó: ΔBFC vuông tại F(Định lí)
\(\Leftrightarrow BF\perp CF\)
\(\Leftrightarrow BF\perp AC\)
\(\Leftrightarrow\widehat{AFB}=90^0\)
hay \(\widehat{AFH}=90^0\)
Xét tứ giác AEHF có
\(\widehat{AEH}\) và \(\widehat{AFH}\) là hai góc đối
\(\widehat{AEH}+\widehat{AFH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔABC có
BF là đường cao ứng với cạnh AC(cmt)
CE là đường cao ứng với cạnh AB(cmt)
BF cắt CE tại H(gt)
Do đó: H là trực tâm của ΔABC(Định lí ba đường cao của tam giác)
\(\Leftrightarrow AH\perp BC\)
hay \(AD\perp BC\)(đpcm)

a: Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH\(\perp\)BC
ít tra mạng xong tham khảo đi ạ
nếu bạn làm được thì bạn hãy làm đi , tra mạng , và tham khảo ít thôi nhé