Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi M là trung điểm của BC
Xét ΔABC có G là trọng tâm
nên AG=2GM
=>GG'=2GM
hay M là trung điểm của GG'
Xét tứ giác BGCG' có
M là trung điểm của BC
M là trung điểm của GG'
Do đó: BGCG' là hình bình hành
SUy ra: BG'=CG
b: Xét ΔJMC vuông tại M và ΔKMB vuông tại M có
MC=MB
góc JCM=góc KBM
Do đo: ΔJMC=ΔKMB
Suy ra: BK=CJ
c: Ta có: I nằm trên đường trung trực của BC
nên IB=IC

Làm tắt luôn cho nhanh này=,=
a,Gọi D là trug điểm BC
Tam giác BDG'=tam giác CDG(c.g.c)-->BG'=GC
b,Tam giác vuông DBK=tam giác vuông DIC(g.c.g)-->BK=JC
c,BI=IC(I thuộc trung trục BC)
tương tự JC=JB\Rightarrow góc IBJ=góc ICJ(bằng hiệu các góc bằng nhau)

Làm tắt luôn cho nhanh này=,=
a,Gọi D là trug điểm BC
Tam giác BDG'=tam giác CDG(c.g.c)-->BG'=GC
b,Tam giác vuông DBK=tam giác vuông DIC(g.c.g)-->BK=JC
c,BI=IC(I thuộc trung trục BC)
tương tự JC=JB\Rightarrow góc IBJ=góc ICJ(bằng hiệu các góc bằng nhau)

Trên đường trung tuyến AD có điểm G thỏa mãn: 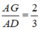
Suy ra: G là trọng tâm tam giác ABC.
Do tia BG cắt AC tại E nên E là trung điểm của AC.
Do tia CG cắt AB tại F nên F là trung điểm của AB.
Theo tính chất trọng tâm tam giác ta có:
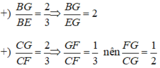
Chọn (B)
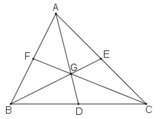
a: Xét ΔABC có
BN là đường trung tuyến
AM là đường trung tuyến
BN cắt AM tại G
Do đó: G là trọng tâm của ΔABC
=>AG=2GM
mà AG=GG'
nên GG'=2GM
=>M là trung điểm của GG'
b: Xét tư sgiác BGCG' có
M là trung điểm của BC
M là trung điểm của GG'
Do đó: BGCG' là hình bình hành
Suy ra: CG=BG' và CG//BG'