Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Ta có:
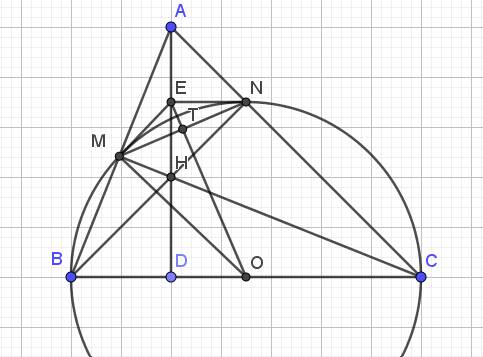
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$

ABCOMNHE
a) Do M, N thuộc đường tròn đường kính BC nên \(\widehat{BMC}=\widehat{BNC}=90^o\Rightarrow BN\perp AC;CM\perp AB\)
Xét tam giác ABC có BN và CM là hai đường cao nên H là trực tâm, vậy thì AH cũng là đường cao của tam giác hay \(AH\perp BC\)
b) Do AMH và ANH là các tam giác vuông có chung cạnh huyền AH nên AMHN là tứ giác nội tiếp đường tròng tâm E, bán kính EH. Vậy thì \(\widehat{MHE}=\widehat{MNA}\) (Hai góc nội tiếp cùng chắn cung AM)
Lại có EM = EH nên \(\widehat{MHE}=\widehat{HME}\)
Vậy nên \(\widehat{HME}=\widehat{MNA}\) (1)
Lại có do OM = OC nên \(\widehat{OMC}=\widehat{OCM}\) mà \(\widehat{OCM}=\widehat{BNM}\) (Hai góc nội tiếp cùng chắn cung BM)
Vậy nên \(\widehat{OMC}=\widehat{BNM}\) (2)
Từ (1) và (2) suy ra \(\widehat{HME}+\widehat{OMC}=\widehat{MNA}+\widehat{MNB}\Rightarrow\widehat{EMO}=\widehat{ANH}=90^o\)
Vậy ME là tiếp tuyến của đường tròn (O)
Xét tam giác MEO và NEO có: Cạnh EO chung, EM = EN, OM = ON
\(\Rightarrow\Delta MEO=\Delta NEO\left(c-g-c\right)\)
\(\Rightarrow S_{MEO}=S_{NEO}\Rightarrow S_{MEO}=\frac{1}{2}S_{MENO}\)
\(\Rightarrow\frac{1}{2}ME.MO=\frac{1}{4}.MN.EO\Rightarrow MN.OE=2ME.MO\)
c) Do tứ giác AMHN nội tiếp nên \(\widehat{MAH}=\widehat{MNH}\)
Mà \(\widehat{MCB}=\widehat{MNH}\Rightarrow\widehat{MAH}=\widehat{MCB}\)
Vậy thì \(\Delta AMH\sim\Delta CMB\left(g-g\right)\Rightarrow\frac{CM}{AM}=\frac{CB}{AH}=1\)
Lại có xét tam giác vuông AMC, \(tan\widehat{BAC}=\frac{MC}{AM}=1.\)

a: Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔBAC có
BN là đường cao ứng với cạnh huyền AC
CM là đường cao ứng với cạnh huyền AB
BN cắt CM tại H
Do đó: AH⊥BC

Câu hỏi của Nhóc vậy - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo câu tương tự tại đây.
Với câu c, ta thấy \(sin\widehat{BAC}=\frac{\sqrt{2}}{2}\Rightarrow\widehat{BAC}=45^o\Rightarrow tan\widehat{BAC}=1\Rightarrow\frac{BC}{AH}=1\)
Vậy AH = BC.
B M A E H O I C
b) Ta có : EA = EH ( gt )
Xét : tam giác MHA vuông tại M . có ME là trung tuyến
\(\Rightarrow ME=\frac{1}{2}AH\Rightarrow ME=EH\)
\(\Rightarrow\Delta MEH\)cân tại E
\(\Rightarrow\widehat{EMH}=\widehat{H_1}\left(1\right)\)
Ta lại có : \(OM=OC\left(=bk\right)\Rightarrow\Delta OMC\)cân tại O
\(\widehat{OMC}=\widehat{OCM}\left(2\right)\)
Mặt khác : Tam giác IHC vuông tại I => \(\widehat{ICM}+\widehat{H_1}=90^o\)
mà \(\widehat{H_1}=\widehat{H_2}\)( đối đỉnh ) \(\Rightarrow\widehat{ICM}+\widehat{H_2}=90^o\left(3\right)\)
Từ (1)(2) và (3) => \(\widehat{OMC}+\widehat{EHM}=90^o\)
mà \(\widehat{OME}=\widehat{OMC}+\widehat{EHM}=90^o\)
\(\Rightarrow ME\perp OM\)tại M
Vậy : ME là tiếp tuyến của đường tròn tâm O ( đpcm )

AH = BC => tam giác MBC =MHA ( tự cm)
=> BMH vuông cân tại M => NBA = BAN = 45
=>...

a: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
=>CM\(\perp\)MB tại M
=>CM\(\perp\)AB tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đó ΔBNC vuông tại N
=>BN\(\perp\)NC tại N
=>BN\(\perp\)AC tại N
Xét ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
Do đó: H là trực tâm của ΔABC
b: Gọi K là giao điểm của AH và BC
Xét ΔABC có
H là trực tâm của ΔABC
K là giao điểm của AH và BC
Do đó: AH\(\perp\)BC tại K
Ta có: ΔAMH vuông tại M
mà ME là đường trung tuyến
nên EM=EH
=>ΔEMH cân tại E
=>\(\widehat{EMH}=\widehat{EHM}\)
mà \(\widehat{EHM}=\widehat{KHC}\)(hai góc đối đỉnh)
và \(\widehat{KHC}=\widehat{ABC}\left(=90^0-\widehat{MCB}\right)\)
nên \(\widehat{EMH}=\widehat{ABC}\)
Ta có: OM=OC
=>ΔOMC cân tại O
=>\(\widehat{OMC}=\widehat{OCM}\)
Ta có: \(\widehat{EMO}=\widehat{EMH}+\widehat{OMC}\)
\(=\widehat{ABC}+\widehat{OCM}\)
\(=90^0\)
=>ME là tiếp tuyến của (O)
c: Gọi I là giao điểm của EO và MN
Ta có: ΔHAN vuông tại N
mà NE là đường trung tuyến
nên NE=AE=ME
Ta có: NE=ME
=>E nằm trên trung trực của NM(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OE là đường trung trực của MN
=>OE\(\perp\)MN tại trung điểm I của MN
Xét ΔMEO vuông tại M có MI là đường cao
nên \(MI\cdot EO=ME\cdot MO\)
=>\(2\cdot MI\cdot EO=2\cdot ME\cdot MO\)
=>\(MN\cdot OE=2\cdot ME\cdot MO\)