Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

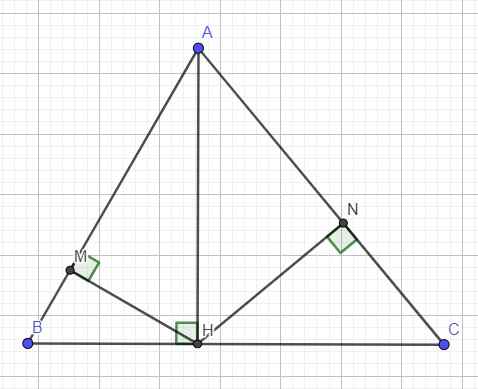
Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao BM:
\(AH^2=AM.AB\) (1)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao CN:
\(AH^2=AN.AC\) (2)
(1);(2)\(\Rightarrow AM.AB=AN.AC\)

a: ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
=>góc AMN=góc ACB
=>góc NMB+góc NCB=180 độ
=>NMBC nội tiếp
b: kẻ đường kính AL
góc ACL=90 độ
AC*AN=AH^2
ΔAIN đồng dạng với ΔACE
=>AI/AC=AN/AE
=>AI*AE=AH^2
góc ADE=90 độ
=>ΔADE vuông tại D
=>AI*AE=AD^2=AH^2
=>AD=AH

a, Xét tứ giác ADHE ta có
^ADH + ^AEH = 1800
mà 2 góc này đối
Vậy tứ giác ADHE là tứ giác nt 1 đường tròn
b, Ta có \(AH^2=AD.AB;AH^2=AE.AC\) ( hệ thức lượng )
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)Xét tam giác ADE và tam giác ACB
có ^A _ chung ; AD/AC = AE/AB
Vậy tam giác ADE ~ tam giác ACB (g.g)
=> ^ADE = ^ACB
mà ^ADE là góc ngoài đỉnh D
Vậy tứ giác BDEC nt 1 đường tròn