Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

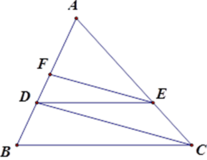
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F . A B = A D 2
Vậy 9.16 = A D 2 ó A D 2 = 144 ó AD = 12
Đáp án: C

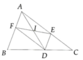
a. Xét tam giác ABC có:
DE//BC (gt)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)(định lý Ta-let) (1)
Xét tam giác ADE có:
AD//CF (gt)
=>\(\dfrac{EA}{EC}=\dfrac{DE}{EF}\)(định lý Ta-let) (2)
Từ (1) và (2) suy ra:\(\dfrac{DA}{DB}=\dfrac{ED}{FE}\)

Bài làm
Xét tam giác ABC có
MN // BC
Theo định lí Thales đảo có:
AM/AB = AN/AC. (1)
Xét tam giác APC có
BN // PC
Theo định lí Thales đảo có:
AB/AP = AN/AC. (2)
Từ (1) và (2) => AM/AB = AB/AP => AB² = AM . AP ( đpcm )

Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I

a) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\) (Pytago).
Thay: \(BC^2=3^2+4^2.\)
\(\Rightarrow BC=5\left(cm\right).\)
Xét \(\Delta ABC:\)
BD là đường phân giác (gt).
\(\Rightarrow\dfrac{AD}{CD}=\dfrac{AB}{BC}\) (Tính chất đường phân giác).
\(\Rightarrow\dfrac{AD}{CD+AD}=\dfrac{AB}{BC+AB}.\)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AB}{BC+AB}.\)
Thay: \(\dfrac{AD}{4}=\dfrac{3}{5+3}.\)
\(\Rightarrow AD=1,5\left(cm\right).\)
\(\Rightarrow CD=BC-AD=5-1,5=3,5\left(cm\right).\)
b) Xét \(\Delta ABC:\)
DK // AB (gt).
\(\Rightarrow\dfrac{BK}{CK}=\dfrac{AD}{CD}\left(Talet\right).\)
Mà \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\left(cmt\right).\)
\(\Rightarrow\dfrac{BK}{CK}=\dfrac{AB}{BC}.\\ \Rightarrow BK.BC=AB.CK.\)