Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

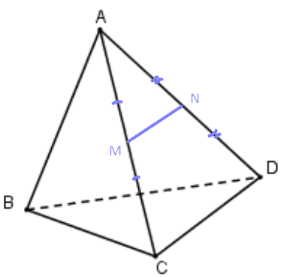
a) Ta có AM cắt (BCD) tại C suy ra AM không song song với (BCD).
b) M, N là trung điểm của AC, AD nên MN là đường trung bình của tam giác ACD suy ra MN // CD.
Mà CD thuộc (BCD) nên MN // mp(BCD).

1:
a: \(D\in SA\subset\left(SAB\right);E\in SB\subset\left(SAB\right)\)
Do đó: \(DE\subset\left(SAB\right)\)
b: \(F\in AB\subset\left(SAB\right)\)
\(F\in DE\subset\left(CDE\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(CDE\right)\)
2:
\(N\in AB\subset\left(ABM\right);N\in CD\subset\left(SCD\right)\)
Do đó: \(N\in\left(ABM\right)\cap\left(SCD\right)\)
\(M\in SC\subset\left(SCD\right);M\in MB\subset\left(ABM\right)\)
Do đó: \(M\in\left(ABM\right)\cap\left(SCD\right)\)
Do đó: \(\left(ABM\right)\cap\left(SCD\right)=MN\)

Tham khảo:
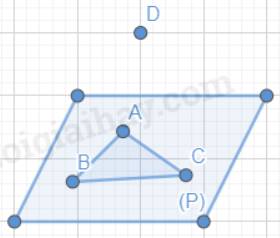
Tồn tại một và chỉ 1 mặt phẳng chứa hai đường thẳng AD và BD

Tham khảo:
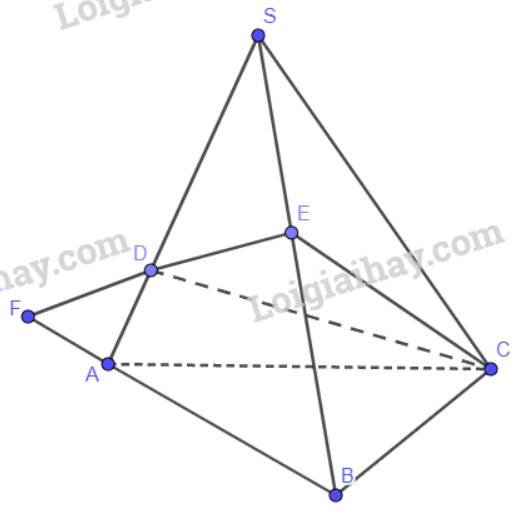
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).

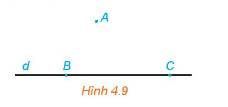
Mặt phẳng (ABC) chứa điểm A và đường thẳng d.
Do đó mp(ABC) cũng chứa hai đường thẳng AB và BC.

Đáp án A
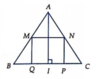
Gọi cạnh hình vuông là x. Ta có ![]()
![]()
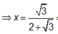
![]()
Gọi V 1 là thể tích hình nón khi quay tam giác ABC quanh trục trung tuyến AI , V 2 là thể tích hình trụ khi quay hình vuông MNPQ quanh trục AI thì
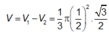
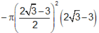
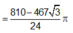

a thuộc (Q) suy ra nếu a cắt (P) thì M thuộc giao tuyến của (Q) và (P) hay a thuộc b.
Tuy nhiên a // b suy ra không thể xảy ra trường hợp a cắt (P).
Kết luận: Nếu a không nằm trong (P) và song song với b thuộc (P) thì a song song với (P) hay a và (P) không có điểm chung.

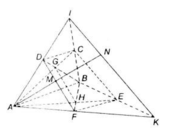
a) Giao tuyến của các cặp mặt phẳng
*Giao tuyến của (AEC) và (BFD)
• Trong hình thang ABCD, AC cắt DB tại G, ta có:
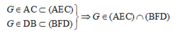
Tương tự, AE cắt BF tại H,
Ta có :
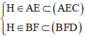 ⇒ H ∈ (AEC) ∩ (BFD).
⇒ H ∈ (AEC) ∩ (BFD).
Vậy GH = (AEC) ∩ (BFD)
*Giao tuyến của (BCE) và (ADF)
Trong hình thang ABCD, BC cắt AD tại I, ta có: I ∈ (BCE) ∩ (ADF)
Trong hình thang ABEF, BE cắt AF tại K, ta có: K ∈ (BCE) ∩ (ADF)
Vậy IK = (BCE) ∩ (ADF)
b) Giao điểm của AM với mp(BCE)
Trong mp(ADF), AM cắt IK tại N, ta có:
N ∈ IK ⊂ (BCE)
Vậy N = AM ∩ (BCE).
c) Giả sử AC cắt BF.
⇒ Qua AC và BF xác định duy nhất 1 mặt phẳng.
Mà qua A và BF có duy nhất mặt phẳng (ABEF)
⇒ AC ⊂ (ABEF)
⇒ C ∈ (ABEF) (Vô lý).
Vậy AC và BF không cắt nhau.
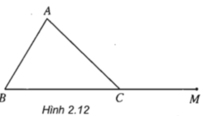
M ∈ BC mà BC ∈ (ABC) nên M ∈ (ABC)
Vì A ∈ (ABC) và M ∈ (ABC) nên mọi điểm thuộc AM đều thuộc (ABC) hay AM ⊂ (ABC)