
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: XétΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
=>AB=AD
b: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)
nên ΔABD đều
c: Ta có: ΔABD đều
=>\(\widehat{DAB}=60^0\)
Ta có: \(\widehat{DAB}+\widehat{DAC}=\widehat{BAC}\)
=>\(\widehat{DAC}=90^0-60^0=30^0\)
Xét ΔDAC có \(\widehat{DAC}=\widehat{DCA}\left(=30^0\right)\)
nên ΔDAC cân tại D
=>DA=DC
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
\(\widehat{HDA}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDHA=ΔDEC
=>AH=EC
d: Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
=>\(\dfrac{AH}{5}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AH=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
XétΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{5}{BC}=sin30=\dfrac{1}{2}\)
=>BC=5*2=10(cm)

Gọi I là giao điểm của AH và BC
Áp dụng định lí pytago trong tam giác vuông ABI ta có
BI2=AB2-AH2
BI2=8.52-42=56.25
BI=căn bậc hai của 56.25
Áp dụng định lí pytago trong tam giác vuông AIC ta có
IC^2=AC^2-AI^2
HC^2=5^2-4^2=9
HI=3
Ta co BI+IC=BC
7.5+3=10.5
Chu vi của tam giác ABC là 8.5+5+10.5=24

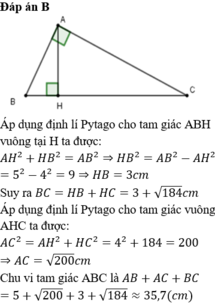
Áp dụng định lí Py-ta-go vào tam giác AHB vuông tại H có:
\(AB^2=AH^2+BH^2\)
=>\(BH^2=AB^2-AH^2=\left(8,5\right)^2-4^2=72.25-16=56.25\)
=> \(BH=\sqrt{56,25}=7.5\)
Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H có:
\(AC^{2^{ }}=AH^2+HC^2\)
=>\(HC^2=AC^2-AH^2=5^2-4^2=25-16=9\)
=>\(HC=\sqrt{9}=3\)
Vì H thuộc BC => BC=HB+HC=7.5+3=10.5
Chu vi tam giác ABC là: AB+AC+BC=8,5+5+10,5=24(cm)
Vậy chu vi tam giác ABC là 24 cm
Kết quả không phải là 24 cm. Vì H nằm ngoài đoạn thẳng BC.