Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

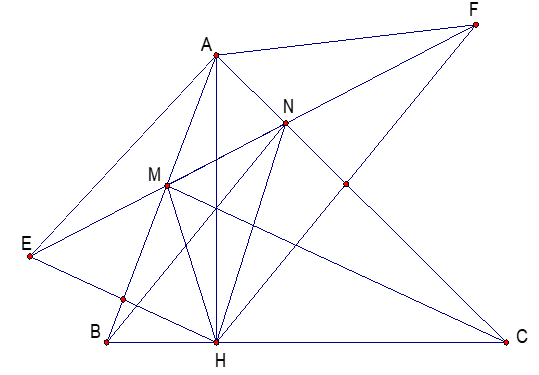
a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2
Từ (1) và (2) suy ra: AE = AF
b.

c.


a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2)
Từ (1) và (2) suy ra: AE = AF
b.
. 
c.


https://olm.vn/hoi-dap/tim-kiem?q=cho+tam+gi%C3%A1c+ABC+(+g%C3%B3c+BAC=+90+%C4%91%E1%BB%99+)+,+AH+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC.g%E1%BB%8Di+E+v%C3%A0+F+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+l%C3%A0+c%C3%A1c+%C4%91i%E1%BB%83m+%C4%91%E1%BB%91i+x%E1%BB%A9ng+c%E1%BB%A7a+H+qua+AB;AC+.+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+EF+c%E1%BA%AFt+B;C+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+t%E1%BA%A1i+M+v%C3%A0+N+.CMR+:+a)+AE=AFB)+HA+l%C3%A0+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+MHNc)+Chung+minh+:+CM+song+song+v%E1%BB%9Bi+EH&id=455200
Bạn tham khảo đường link trên nha, kéo xuống bên dưới đó, mình giải đc rồi nhưng dài quá ko gõ đc :))
À ở câu a) thì cách làm ở link trên đúng và ngắn hơn cách mình làm, còn đây là câu a) của mình nè:
a) Gọi EH cắt AB tại X, FH cắt AC tại Y
Vì E đối xứng với H qua AB nên EH vuông góc AB; EX=XH
Xét tam giác AEX và AHX có:
AX: cạnh chung
EX=XH (cmt)
Góc EXA = góc AXH (=90°)
Suy ra: tam giác AEX = tam giác AHX (c-g-c)
Do đó: AE=AH (2 cạnh tương ứng) (1)
Vì F đối xứng với H qua AC nên FH vuông góc AC; HY=YF
Xét tam giác AHY và AFY có:
HY=YF (cmt)
AY: cạnh chung
Góc AYH = góc AYF (=90°)
Suy ra: tam giác AHY = tam giác AFY (c-g-c)
Do đó: AH=AF (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra: AE=AF(=AH) (đpcm)
*Bạn tự viết kí hiệu góc, tam giác,...v.v... dùm mình nha, mình ko biết viết*
Answer:
(Mình làm bài tắt bạn nhé, khi giải thì bạn ghi đủ ý để tránh bị trừ điểm. Hình bạn tự vẽ.)
a. E đối xứng với H qua AB => AB là đường trung trực của EH => AE = AH
F đối xứng với H qua AC => AC là đường trung trực của HF => AH = AF
=> AE = AF
b. Tam giác AME = tam giác AMH (c.c.c) => Góc AEM = góc AHM
Tam giác ANF = tam giác ANH (c.c.c) => Góc ANF = góc AHN
Mà góc AEM = góc AFN
=> Góc AHM = góc AHN
=> HA là phân giác góc MHN
c. Chứng tỏ tương tự
=> MC và NB lần lượt là phân giác của góc NMH và góc MNH
Có: góc EMH + góc HMN = 180 độ
\(\Rightarrow2\widehat{BMH}+2\widehat{HMC}=180^o\)
\(\Rightarrow2\left(\widehat{BMH}+\widehat{HMC}\right)=180^o\)
=> Góc BMH + góc HMC = 90 độ hay góc BMC = 90 độ
=> CM vuông góc AB mà EH vuông góc AB
=> CM // EH
Chứng minh tương tự => BN // FH